As we saw previously with the scattering formula for charged particle, the scattering of a particle depend strongly of its mass and velocity (and the charge z) :
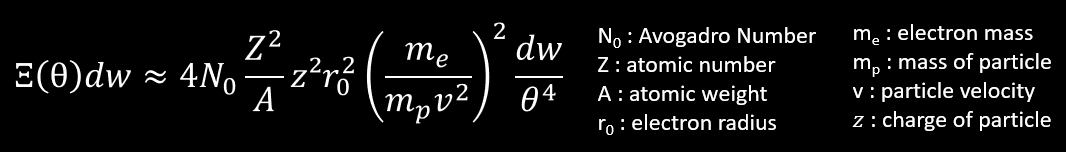
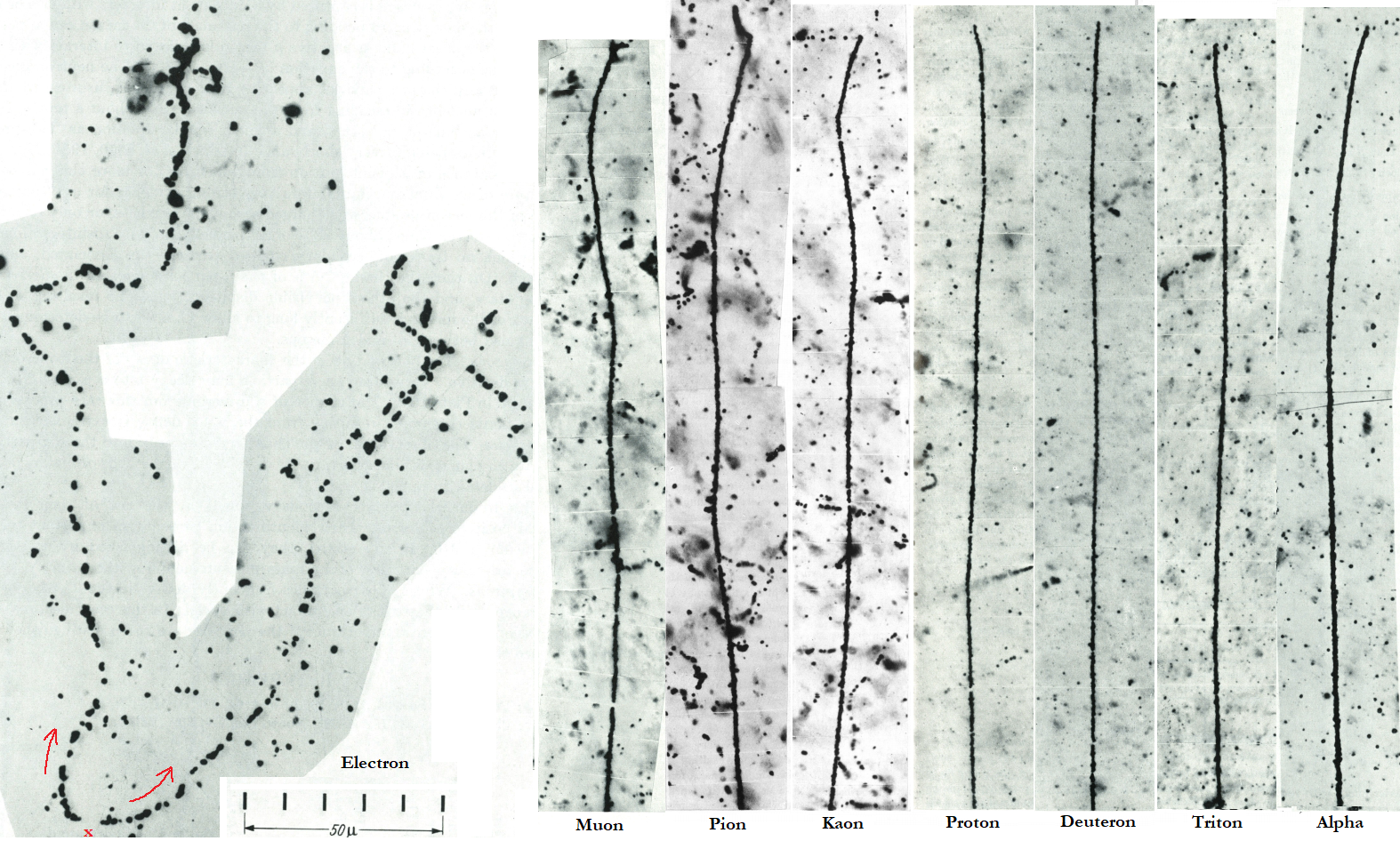
The next picture show the end of range of some particles to compare the scattering effect, in nuclear emulsion.
Upper image : Electrons – A pair of electrons of low energy appears to originate at a point ‘x’ in the lower left hand corner of the photograph. The pair may originate from the materialization of a photon in the Coulomb field of a nucleus. The particles are much scattered owing to their small mass. They become heavily ionizing and thus produce tracks with large grain-density, only over a short path at the end of their range. In passing through a material medium, an electron loses energy not only by ionization, but also by producing quanta in interactions with charged particles (nucleus, atomic electrons…) along its line of motion, by ‘bremsstrahlung‘. The probability of such a process varies with the square of the charge of the particle. It follows that bremsstrahlung commonly results from interactions with nuclei and rarely from interactions with electrons. The production of bremsstrahlung by an electron may result in the loss of a considerable fraction of its energy in a single interaction. Large losses may also occur in direct collision with other electrons (example), but this is a rare process. Electrons can also loses energy by making rarely trident production.
Muon – The pronounced scattering of the particles, as compared with protons, allows the tracks to be distinguished easily. Large deviations due to scattering are clearly more frequent towards the end of the range. When a positive muon reaches the end of its range, it decays into an electron (more precisely, a positon) and in well-developed electron sensitive emulsions, the track of the secondary particle can be distinguished (this is not the case in the picture, so the lack of this electron may come from another process like muon capture). For negative muon on average, 40% of the muons brought at rest decay in orbit (forming a muonic atom) and 60% are captured by the nucleus. This is specific for negative muon as the nucleus attract the particle through the electrostatic forces when the muon is at rest, i.e with no kinetic energy (positive muon are repelled by nucleus and thus undergo decay). When captured by a nucleus, the muon interact with a proton leaving the nucleus in an excited state and producing a neutrino. The main mechanism of de-excitation after muon capture is neutron emission, but charged particles can also be emitted.
Pions – The π– particles produce characteristic nuclear disintegrations at the end of their range. If two or more secondary charged particles are emitted, it’s highly probable (in plates exposed to cosmic rays), that the incident particle was a π– . But it may also due to the capture of a μ– which produced a two prong stars . In such events, however, the energy of the two charged particles is generally very small, thus their range is less than commonly observed in the ‘two prong’ stars produced by π–. For plates exposed to cosmic rays, about 28% of π– particles produce disintegrations at the end of their range with which no tracks of secondary particles are associated and only 25% produce one such track. On the other hand, 7,5 % of μ– arrested in AgBr crystals produce one-prong stars, and the others no visible disintegration. π+ particles, brought to rest, makes characteristic decay into π+→ μ++υμ , the μ+ making ~600 μm range in emulsion.
Kaons – The kaon can decay into one muon or electron or in one or several pions.
Scattering of the particles – The scattering increase inversely with the mass and the speed^2 of the particle, so the scattering is much more probable when the particle is slow i.e when the particle is at the end of its range. The particle pictured above (except electrons) have the same range in photograph, about 190 μm. The pronounced scattering of slow μ,π approaching the end of their range, in comparison with that of proton, allow to distinguish the particles by measuring the average scattering of each particle. As the proton expect few scattering than the μ,π, this indicate that the proton have a heavier mass. Demonstration of the scattering formula.