Cloudylabs

In a cloud chamber, each reaction between particles  respect the following conservations laws :

• the linear momentum,
• the total energy,
• the angular momentum, 
• the electric charge, 
• the baryon and lepton numbers.

The conservation of momentum is the #1 law to know because most of the events we see in a cloud chamber show this conservation. I will briefly resume the basics of linear momentum conservation to show how it can serve in the studying of cloud chambers pictures.

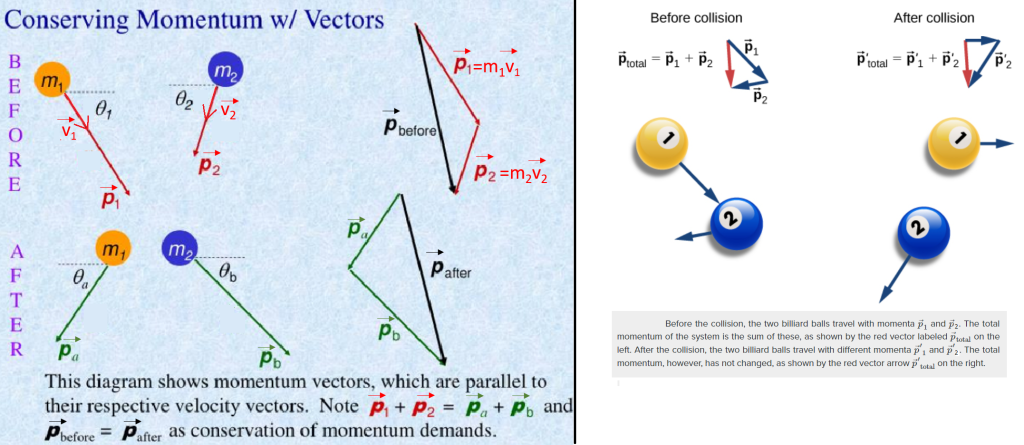
Momentum is a vector quantity : it has both magnitude and direction. Since momentum has a direction, it can be used to predict the resulting direction and speed of motion of particles after they collide (or decay). The momentum of a particle is conventionally represented by the letter p. It is the product of two quantities, the particle’s mass and its velocity (v). So we have p in unit of kg⋅m/s which is the magnitude of the vector.

When an object is in motion and modify its trajectory due to a collision, the momentum vector (before and after the modification of direction) has to be equal. If it’s not the case, then some energy have been lost during the collision, it’s an inelastic collision (some energy can be transfered to excite a particle to other quantum state).

Below, 2 examples of momentum conservation for an elastic collision. Note that the length of vectors depend of the product of mass and velocity of each particles. The additivity of the magnitudes of these vectors give the total momentum of the system before and after collision and we have total momentum initial = total momentum final. 

The resulting particles (after the collision), are still in the same plan X,Y (2D). If more objects are evolved, the conservation of momentum still apply. Example with a exploding bomb. 

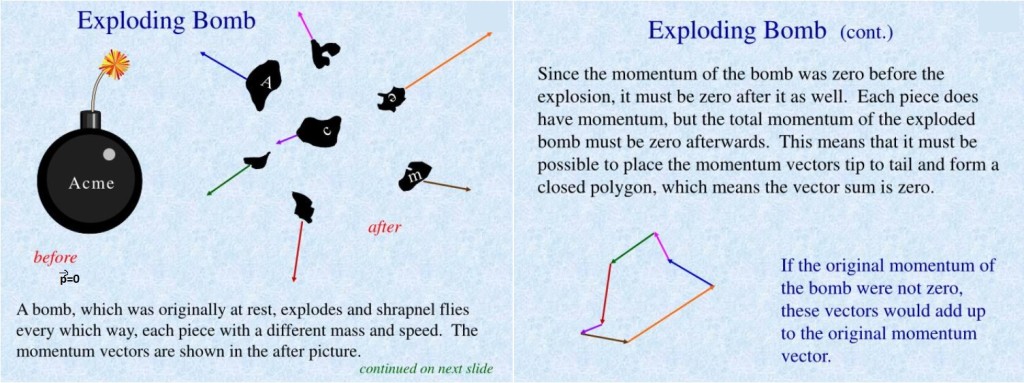
In the picture, the shrapnels go only in the X,Y plan and the momentum after explosion in this plan is still 0. This last example is not the reality of course because shrapnels can go also in the Z direction. But the same conservation of momentum still apply in this direction (Z) and will be 0. Overall, the momentum in each directions will be sum to equal 0, as the initial momentum of the bomb was 0. 

Can we see a « bomb » in a cloud chamber ? Yes, that’s we call a star  or « spallation ». The picture below was taken at 2877 m in a 45×45 cm diffusion cloud chamber. It shows an explosion of a nucleus. The incident particle which caused the spallation is not identified, so it may be a neutral one. In this event, we see about 6 particles in the X,Y plan, the same plan of visibility of the cloud chamber.

But some particles may have travel in the Z direction and we can’t see them because the cloud chamber is not sensitive in this direction (only in X,Y). Even if some particles may be present in the Z direction, the overall momentum of all secondary particles will be equal to the momentum of the incident particle. 

With spallation events, we have to remember that more than 3 particles can be produced by the collision. So some of them can go in the Z direction, and we can’t see them because the cloud chamber is only sensitive to a unique plan X,Y

Spallation is the only case where we are not certain if we are observing all the particles of the event. By chance, most of other nuclear event are limited to 3 particles, and the law of momentum conservation momentum guarantee that we will see the whole events in the same plan.

The common nuclear events which appear in a cloud chamber are :

• Decay of a particle involving 2 daughters particles (for example 220Rn =>  α + 216Po (called recoil nucleus) ],
• Collision of a particle into another.

Let’s consider an event which involve 2 secondary particles. It could be the decay of a particle, for example an hyperon λ⁰ which decay spontaneously into a proton p and a pion π. It could be also a collision between a proton (static or not) with a pion. Or even an alpha decay of a nucleus. This case n°1 is summarized in the left picture, below :

The momentum of the incident particle, A, is in the X direction, or in the X,Y plan. The two secondary particle produced by the event (a decay of A, or an elastic collision of A into a particle B), should conserve the overall momentum (initial and final). It implies that the particles C and D should travels in the XY plan only, as the sum of their momentum vector should be in the X,Y plan, identical to the initial momentum of the A particle. So if you observe in a cloud chamber the particle A and the particle C (or D) you will also see the D (or C) particle.

This works also for the case n°2, where 3 secondary particles are produced, for example in the decay of Kaon into 3 pions. If one of the secondary particle is neutral, you won’t see it in the cloud chamber but the conservation of momentum will be respected. You can see this article which explain how to find neutral particle using momentum conservation. If 3 particles are produced in an interaction, they will also travel in the XY plan to conserve overall momentum.  So if you see A in a cloud chamber and one the 3 secondary particles you will see the rest of particles occurring in the same plan. Note that you will never see a « case n°2 » in a cloud chamber because at sea level it’s very very rare to observe a Kaon decay into 3 pions (plus add 5 % branching ratio, if you see one !). Anyways, « case n°2 » can often happens in a cloud chamber with the beta decay of a nucleus. But you won’t see the neutrino or the recoiling nucleus which have almost no kinetic energy after the reaction.

If more than 3 secondary particles are produced, for example in a spallation, it’s possible that some particles can travel in the Z direction, canceling their momentum vector. So the whole event won’t appear in a unique plan, but in a 3 dimensional system. 

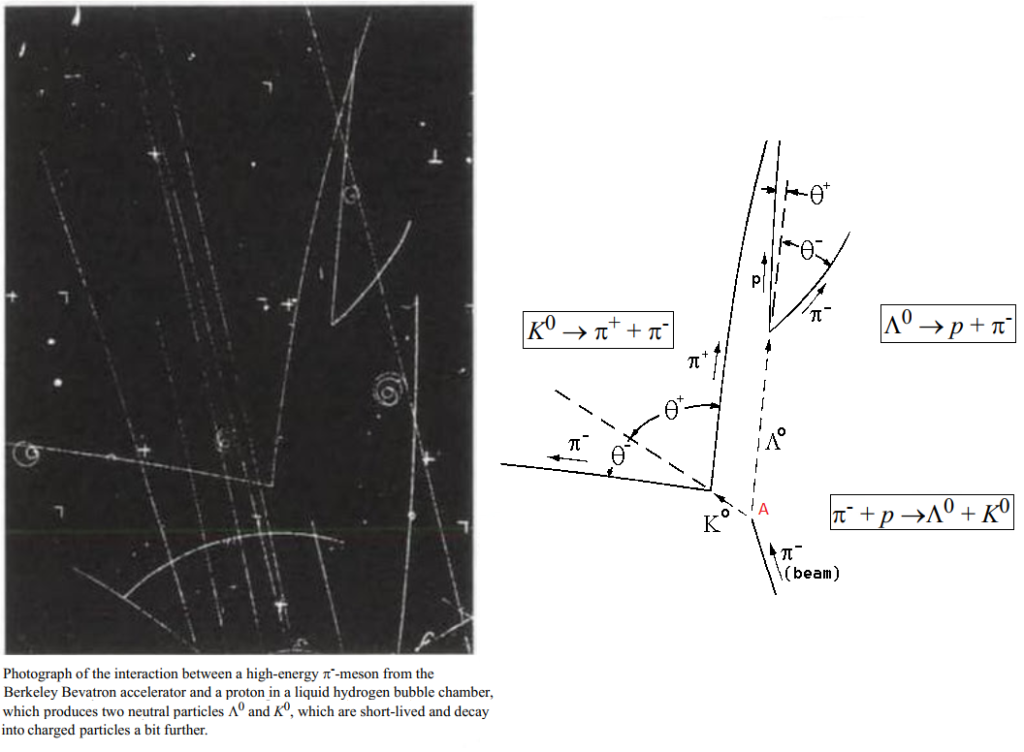
The above picture show a triple « case n°1 » : all the secondary particles are in the same plan of the primary, initial particle :  π^–. The plan of the 3 interactions is mingled with the plan of sensitivity of the bubble chamber. The incoming particles are pions at 1000 MeV/C, coming in the middle, at the bottom of the picture. One of them collide with a proton (p) of the hydrogen (it’s a bubble chamber) in A. This proton is essentially at rest because there is no recoil track. It makes the first collision, producing two neutral particle (a lambda λ⁰ and a kaon K⁰ ). The two neutral particle moved (we can’t see the tracks because their neutrality) then decayed producing pions and a proton. Note that if a neutral particle was produced at rest (kinetic energy=0 like it’s momentum), the two decay products of it would be emitted in opposite directions due to momentum conservation. If a particle move and decay in flight, the decays particles are emitted forward, in the direction of the initial particle (called a boosted particle).

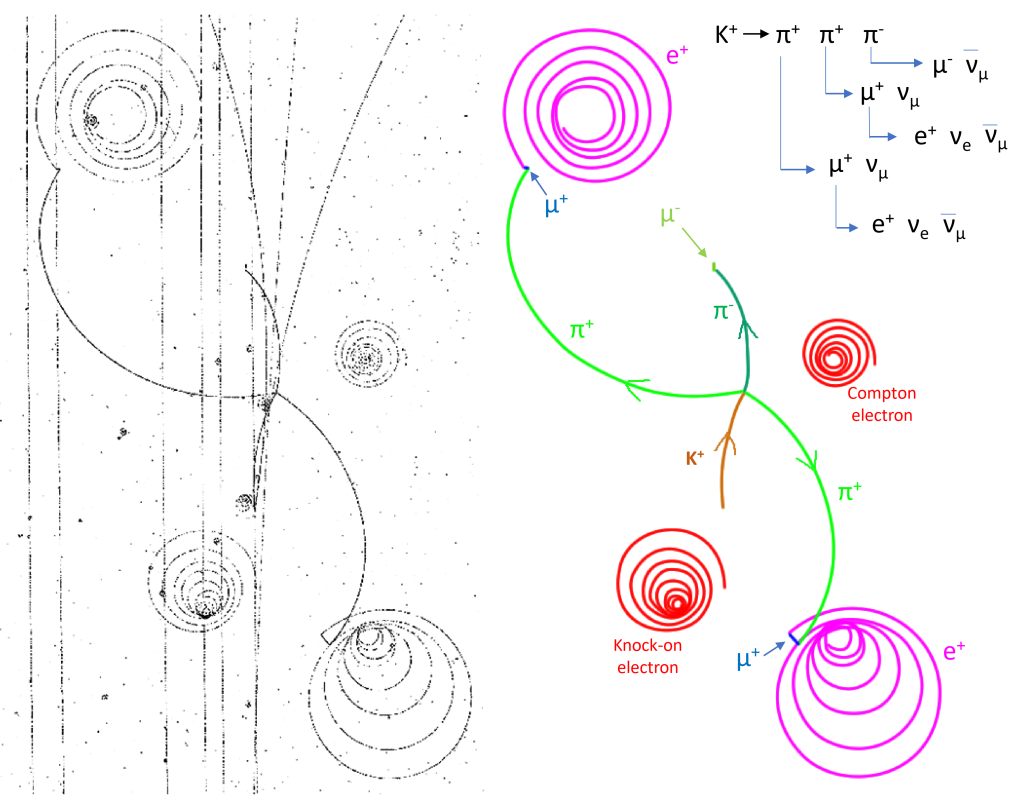
The next picture comes from the CERN 2-metre hydrogen bubble chamber. It was exposed to a beam of positive kaons K⁺with energy 10 GeV entering from the bottom. This picture illustrate a « case n°2 », where all the decay particles of an incoming Kaon are produced in the same plan (happily in the same plan of visibility of the bubble chamber).

In the middle of the picture a K⁺decays into π⁺π⁺π^–. Each pion then stops before decaying into a muon μ. The two positive muons move a short distance before stopping and decaying into spiraling positrons. The negative muon fails to produce an electron because it has gone into the glass window of the bubble chamber. The decay scheme which includes the various unseen neutrinos ν produced in the decays is indicated. A knock-on electron and a lone spiraling ‘Compton’ electron shows that negative particles turns to the left.

Momentum and energy transfer in decay reactions A => B + C  or A => B + C + D  

1) A → B + C, where A is at rest  – Classical approach

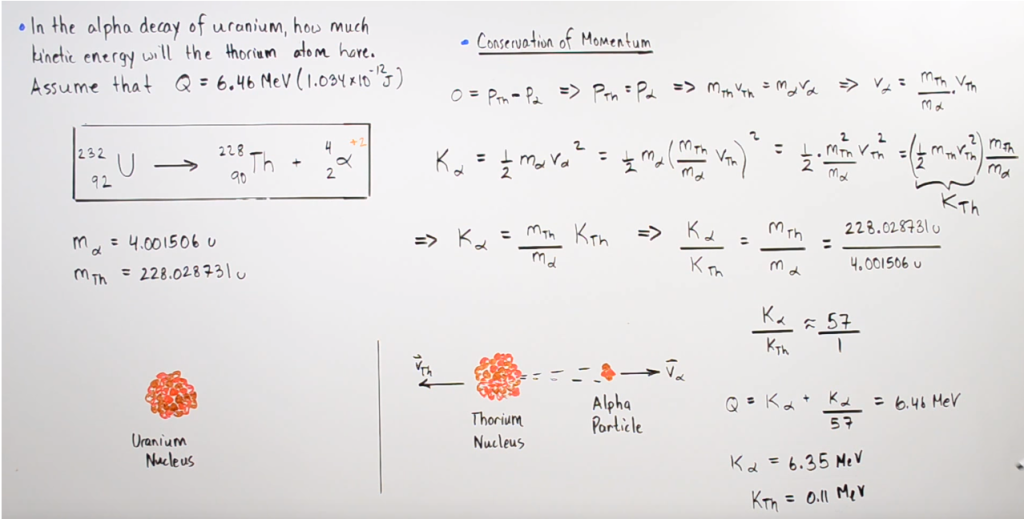
Let’s back to the « case n°1 » involving 2 daughters particles, coming from a decayed parent particle which was at rest (it has no kinetic energy). This reaction is very common in cloud chamber as it’s the alpha decay process. The picture below summarize the energy transfer in the 232 U => 228 Th + α 

 Remember that Q = (∑m_i – ∑m_f)c² =∑K_f – ∑K_i 

As the parent particle (A) is at rest, the two daughter particles [the recoil nucleus 228 Th (C) and the α(B)] are emitted in the opposite direction to conserve the initial momentum of A : 

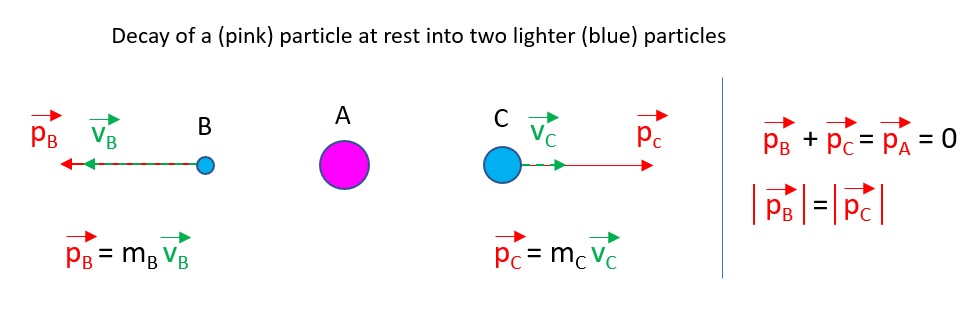
The magnitude of the momentum of each particle is equal. But as the daughter particles have different mass, their speed is necessarily different to conserve the magnitude of momentum. This implies that the lighter particle will have a great kinetic energy coming from the decay process (the daughters particles share the Q of the disintegration reaction), whereas the bigger particle will have a small quantity of kinetic energy.

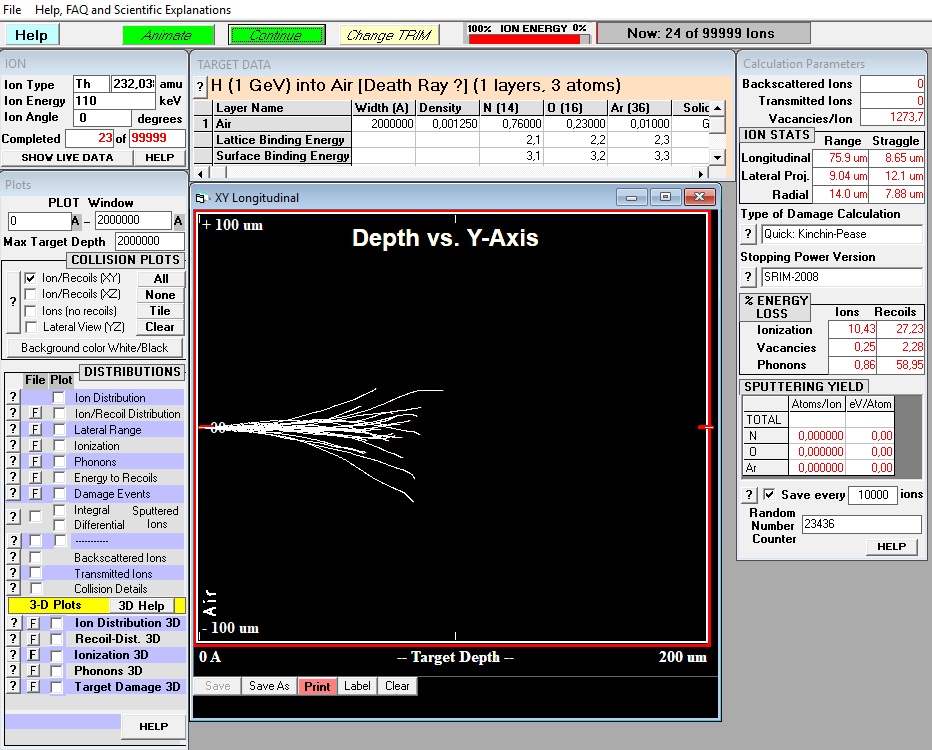
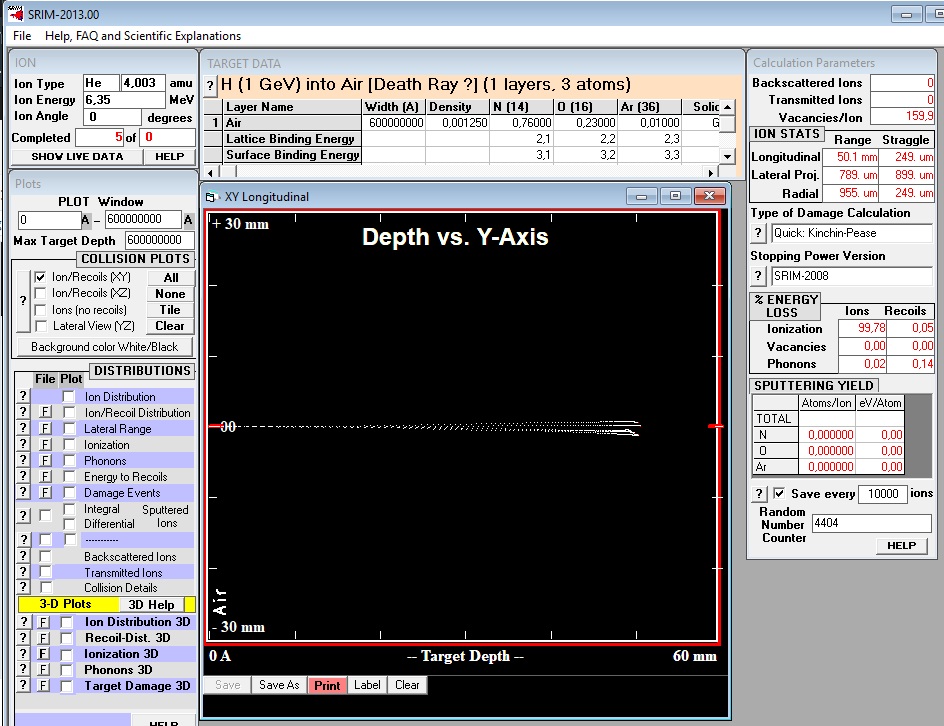
The numerical example with 232 U, shows that the 228Th nucleus receive 0.11 MeV of kinetic energy, whereas the alpha get 6.35 MeV  (it’s an example for a Q reaction of 6.46 MeV, there is also other values of Q for this reaction). What could be the range of a 228Th nucleus of 0,11 MeV of kinetic energy in a cloud chamber ?  For that, we will use the marvelous SRIM software which calculus the range of ions in matter (www.srim.org). Let’s put a nucleus of 228 Th in air, at 100 keV :

This nucleus can travel only about 0,75 mm in air (see « ion stats », longitudinal top right), so we will never observe such recoil nucleus in a cloud chamber. But not really never, if you use a low pressure cloud chamber like Joliot in 1934. Why this so small range ? because this nucleus have a very slow speed and a high charge, and remember that the energy loss is proportionnal to z²/v². What could be the real speed of this nucleus in vacuum ? With m₀ = 228*939, we obtain about 300 km/s. 

What about the alpha particle gaining 6.35 MeV in the reaction ?

The alpha can travel about 5 cm in air. This is commonly observed in a cloud chamber, with the radon decay, or from a radioactive alpha source (mineral of pitchblende, radium hands, thorium rod…)

2) A → B + C, where A is at rest  – Relativistic approach

 In 1), we considered the decay of a particle into two daughters particles, where their velocity are small, that’s to say < 0.1c (c = speed of light). We know that if a particle has a very high speed, we can’t use anymore the classical definition of kinetic energy (Ke=0,5 mv²) because the calculus error are too much. It’s right to use a classical approach for Alpha disintegration because the velocity of daughter particles are <0.05 c. But when the disintegration give daughter particles at relativistic speed, like the pion decay, we have to use the relativist form of kinetic energy.  

Here is the theory to obtain the energy transfered to a particle B or C, from the decay of a particle at rest A (relativist approach). Remember that if we have a 2 body decay, with the parent particle at rest it means that the 2 particles are shoot off in opposite direction.

Now we can consider the decay at rest of a pion into a muon and a neutrino and calculate the velocity of the daughter particles.

This case can be perfectly illustrated with nuclear emulsion able to capture the decay of charged particles, like pions. Emulsion plate are exposed to high altitude and records the tracks of cosmic particles, after being developed. The next picture show the decay of 4 pions into  π^-+→ μ^-++ ν → e^-++2 ν. The neutrino ν, uncharged, are not recorded in the emulsion. In the bottom, an incoming pion loses it’s kinetic energy and comes to rest (we are observing only the last 100 microns of the π track). It decay into a muon (and a neutrino), which travel about 600 micron in the emulsion, then decay into a lepton (electron or positon). The length of the 4 μ are equal : as they are emitted by pions at rest, they have a kinetic energy of 4.1 MeV (as calculated previously). The muon then comes at rest and decay into leptons. What energy gain the lepton after the disintegration of the muon ? as two neutrino are also emitted, it’s a three body decay (see case 3) below). The total energy of the muon (rest mass 105.7 MeV/c²) is shared between the three particles, so the lepton can receive any energy in the range [0-105.7 MeV] assuming the neutrino are massless.

Note that the length of muons are « nearly » the same. Whilst most of the electrons ejected from atoms by the passage of a fast particle are of low energy, occasional electrostatic collisions result in the production of δrays, electrons projected with considerable energy which produce secondary ionization. The production of this δrays involves a corresponding loss of energy of the parent particle, so the overall tracks length of these muons can be sightly different even if the 4 particles have the same initial kinetic energy from the π decays. On the 2nd muon track of the left, mid -range, you can see 2 delta rays about 50-100 keV energy.

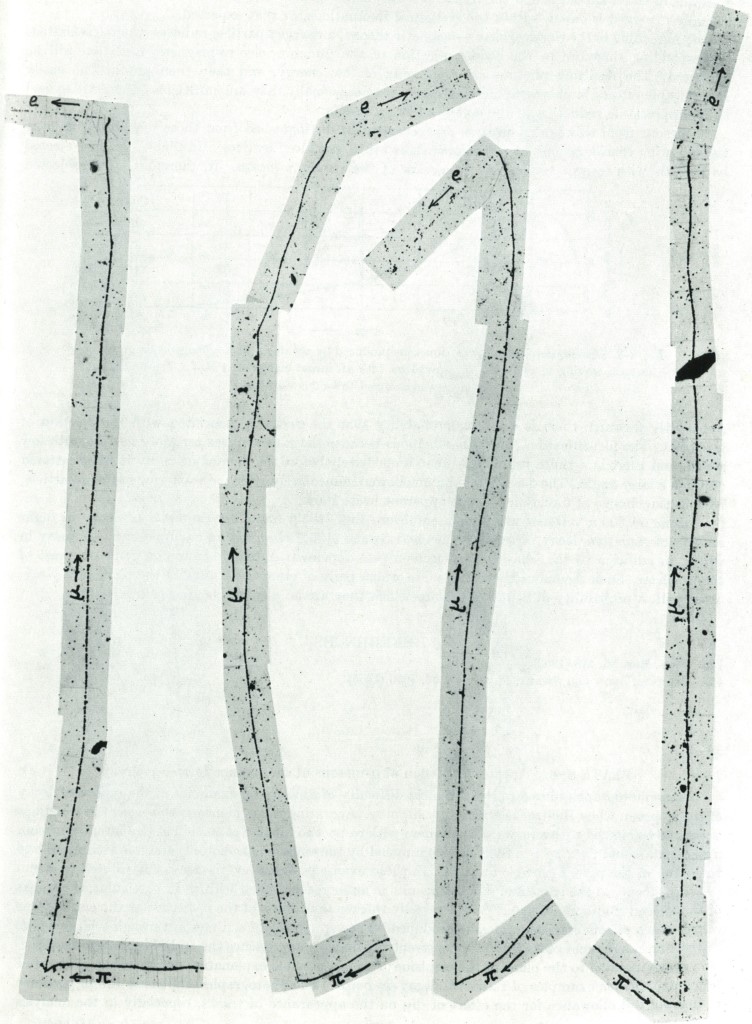
Successive decay of 4 pions at rest. Kodak NT4 emulsion, Powell 1950. The muons tracks are nearly of equal lengths : they have the same kinetic energy. So they come from the decay at rest of pions which disintegrate into two body.

 Of course, charged particles are not obliged to decay at rest and can decay in flight (below).

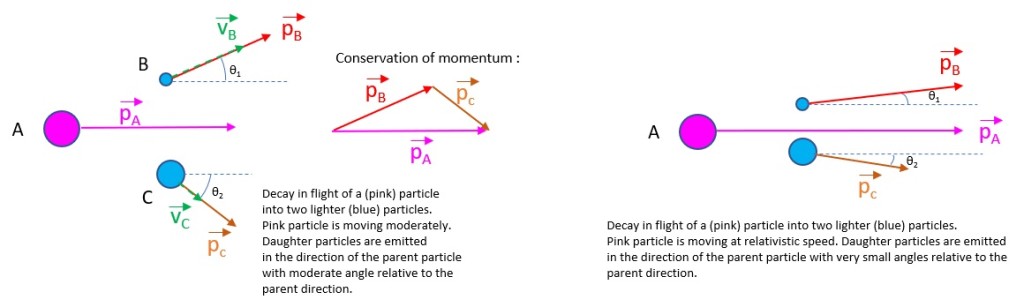
3) A →  B + C, where A is moving  – Decay in flight

When A is at rest and decay, the daughter particles are emitted at 180° each other. But when the parent A particle is moving, the daughter particles will be emitted in the same direction of the initial particle, with an angle relative to the parent’s direction.  The slower the parent particle, the higher the angles of daughters Θ_1,2 and inversely. When the parent particle is traveling at relativistic speed, the daughter particles are almost emitted in a parallel direction of the parent particle (Θ_1,2≈0)

 We can see this phenomenon when a high speed object explode in flight : the fragments are propelled forward, in the direction of the initial object. Example with the Chelyabinsk meteor of 2013 : 

Same occurs for fireworks. When the rocket is fired and explode stationary (just before to fall), the fragments are emitted in any directions and overall momentum is 0 (since the momentum of the stationary rocket is 0). When the rocket explode while moving, the fragments are moved forward the direction of the rocket. The momentum of theses secondaries equal the initial momentum of the rocket. This apply also for spacecraft traveling near c.

 

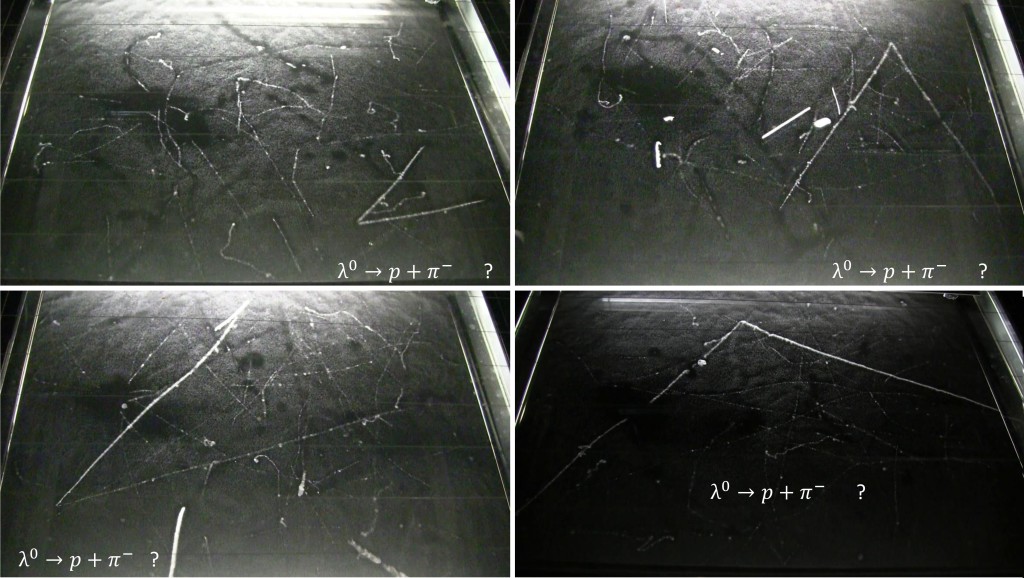
In a cloud chamber, we can see this forward « boost » of daughter particles, with the reaction  λ⁰ → π^–+ p . The decay of the neutral lambda (64% of branching ratio for this reaction) produces two charged particle of different mass (π^–= 139 MeV/c² and p =938 MeV/c²), so the proton will have slightly less velocity than the pion.  It will thus, make a more ionizing track (because energy loss (i.e density of droplets) is ≈ z²/v²). You can see that below, and principally here about the difference of density of ionization left by these 2 particles.

 In 2012, I went to the Pic du Midi (2877 m) and filmed a cloud chamber which was there for the 100th anniversary of the discovery of cosmic rays. I filmed for 8 hours and I checked all frames to find interesting events. As the occurrence of the neutral lambda is much more in altitude than in sea level, I guess I captured at last one event showing this type of decay.

3) A →  B + C + D

Even if the parent particle is at rest or moving, there is a great variety of angles and momentum for each of the products. If the parent particle is moving, these particles will also be boosted in the direction of the parent particle. An example of this reaction is the decay of a Kaon into 3 pions (seen previously in this page), the β^-/+ or μ^-/+ disintegration.

β disintegration

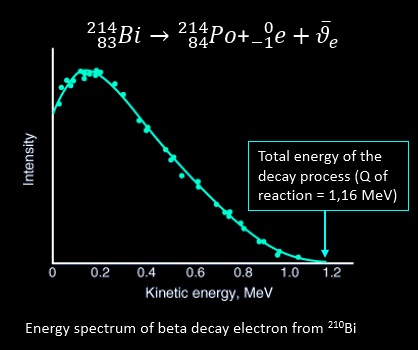
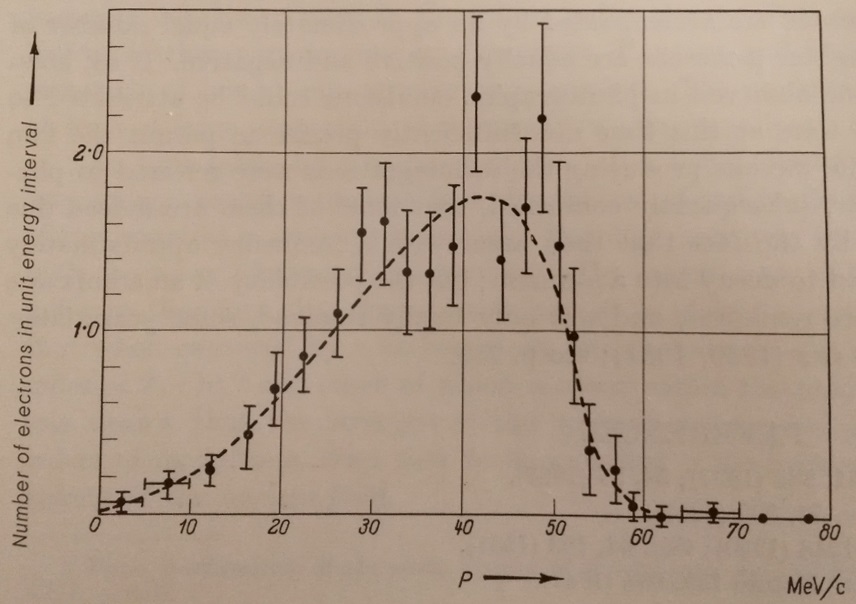
For the β disintegration, the next picture made in 1940 show the number of electron versus their energy from the decay of Radium E (Bi 210) : 

The Q of the reaction is shared between the kinetic energy of the beta particle, the energy of the neutrino, and the kinetic energy of the recoiling daughter nucleus. Thus, the energy of an emitted beta particle can take on a range of values because the energy can be shared in many ways among the three particles while still obeying energy and momentum conservation. The recoiling nucleus get a very small fraction of energy from the process, in the eV range and usually can be ignored. In the above curve, if we observe an electron of 0.40 MeV energy from the beta decay of ²¹⁰Bi this mean that the antineutrino has the remaining energy: 1.16-0.40=0.76 MeV. An electron at the far right of the curve would have the maximum possible kinetic energy, leaving the energy of the neutrino to be only its small rest mass.  The average energy of the beta particle is approximately 1/3 of the maximum energy.

Note that spectral shape of β^– and β⁺ decay is different, due to electrostatic interaction of outgoing electron (positron) and daughter nucleus.

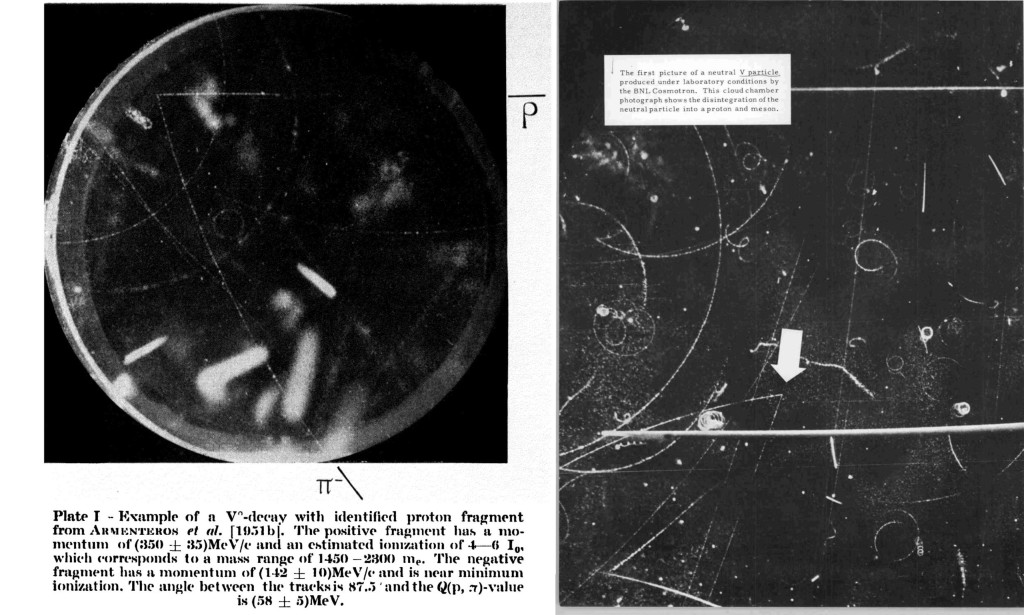
  A recoil nucleus was observed in 1959 in a cloud chamber from the beta decay of  ⁶He  into ⁵Li . This is the picture in left. The electron is the curved track, the recoil nucleus the tiny fat track going in the left.

«  The track of the recoil nucleus is clearly visible. Its direction is usually not directly opposite to that of the β particle: they form an obtuse angle, i.e., it is clearly seen that a certain amount of momentum is missing » 

 The missing momentum has to be ascribed to an uncharged particle traveling upward in the picture.

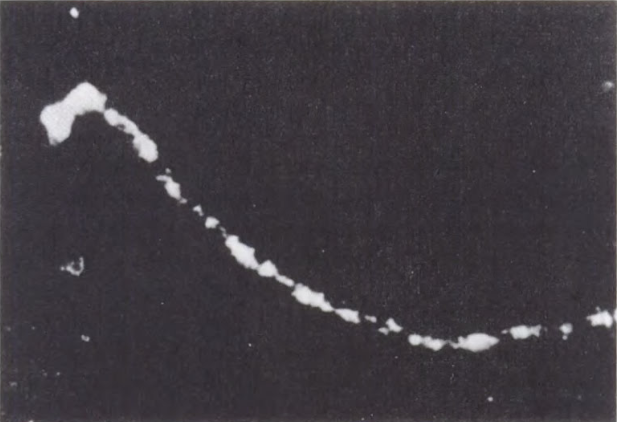
When the μ decays, it emits a charged particle with a velocity approaching that of light.  In the first observation of this phenomenon in 1940 the energy of the secondary particles was estimated to be 70 ± 30 MeV/c. This result suggested hat the muon decays into an electron and a single neutrino, the two particle sharing, almost equally, the energy made available by the disappearance of he rest-mass of the parent particle (105,7 MeV/c²).  It was shown in 1949 with a Wilson chamber and photographic plates (nuclear emulsion) that this view is incorrect.  The later experiments showed that when μ decay ‘at rest’ the energy of the secondary charged particles vary within wide limits as you can see in the left picture.