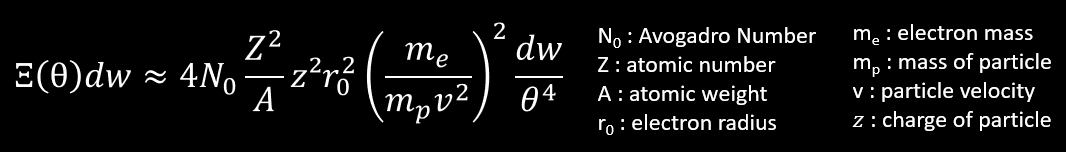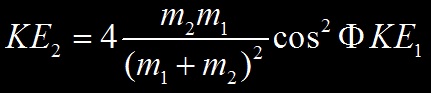Description of the energy losses of a charged particle
The energy loss of a charged particle travelling in matter come from two interaction process : by collision and radiative process. The probability of each process is determined by the distance of approach of the particle to the atom with which it interacts. This distance is called the impact parameter b.
Collision process : If the distance of closest approach is large compared with atomic dimensions (b high), the atom as a whole reacts to the field of the passing particle. The result is an excitation or ionization of the atom. Excitation is much more probable versus ionization, because ionization need more energy than excitation (we will see later that small energy transfer from the incoming particle to atomic electrons is much more probable than high energy transfer). To make an ionization (and thus a ion in which a droplet will form in the cloud chamber), a N2 molecule should receive about 30 eV. These distant encounters are also called « soft collisions ».
If the distance of closest approach is of the order of atomic dimensions, the interaction is between the moving charged particle and one of the atomic electrons. This process results in the ejection of an electron from the atom with considerable energy and is often described as a knock-on process, or « hard collision ». In general, the energy acquired by the secondary electron is large compared with the binding energy. The ejected electron is called a « delta ray (δ-ray) » and can make its own path in matter due to its kinetic energy, given by the incoming particle. Usually an ejected atomic electron is called a delta ray if it gets at last 100 eV during the knock-on process.
What we call collision is in fact an approximation as there is no physical collision between the incoming particle and the target particle (the target can be either an electron of the atom, or a nucleus). All collisions are « electrostatic » and made at various distance, according to the impact parameter b. This is not the case during a nuclear reaction where the incoming particle is physically absorbed by the nucleus (but this is so rare that you will never see that in a common cloud chamber).
Electrostatic « collision ». As b get lower, the deflection of the incoming particle is higher and also the energy loss by radiation
Radiative process : When the distance of closest approach becomes smaller than the atomic radius, the deflection of the particle trajectory in the electric field of the nucleus is the most important effect. This deflection process results in radiative energy losses and the emitted radiation (bremsstrahlung) covers the entire energy spectrum up to the maximum kinetic energy of the charged particle. But this radiative process is less frequent than the collision process because particle have much more chance to pass far from a nucleus than near to it. Radiative losses have almost no effect for heavy, incoming particle but it’s not the case for lightweight particle like electron or positon.
We can illustrate the occurrence of the 2 process of energy loss with a common cloud chamber picture.
In a cloud chamber, we see thousands of droplets building the path of the particle. Theses droplets come from the ions left by the particle travelling in matter, which ionized and excited the atoms. Producing ions require energy, so it’s a loss for the incoming particle. This is the first energy loss process due to the electrostatic « collision » of the incoming particle with the atoms.
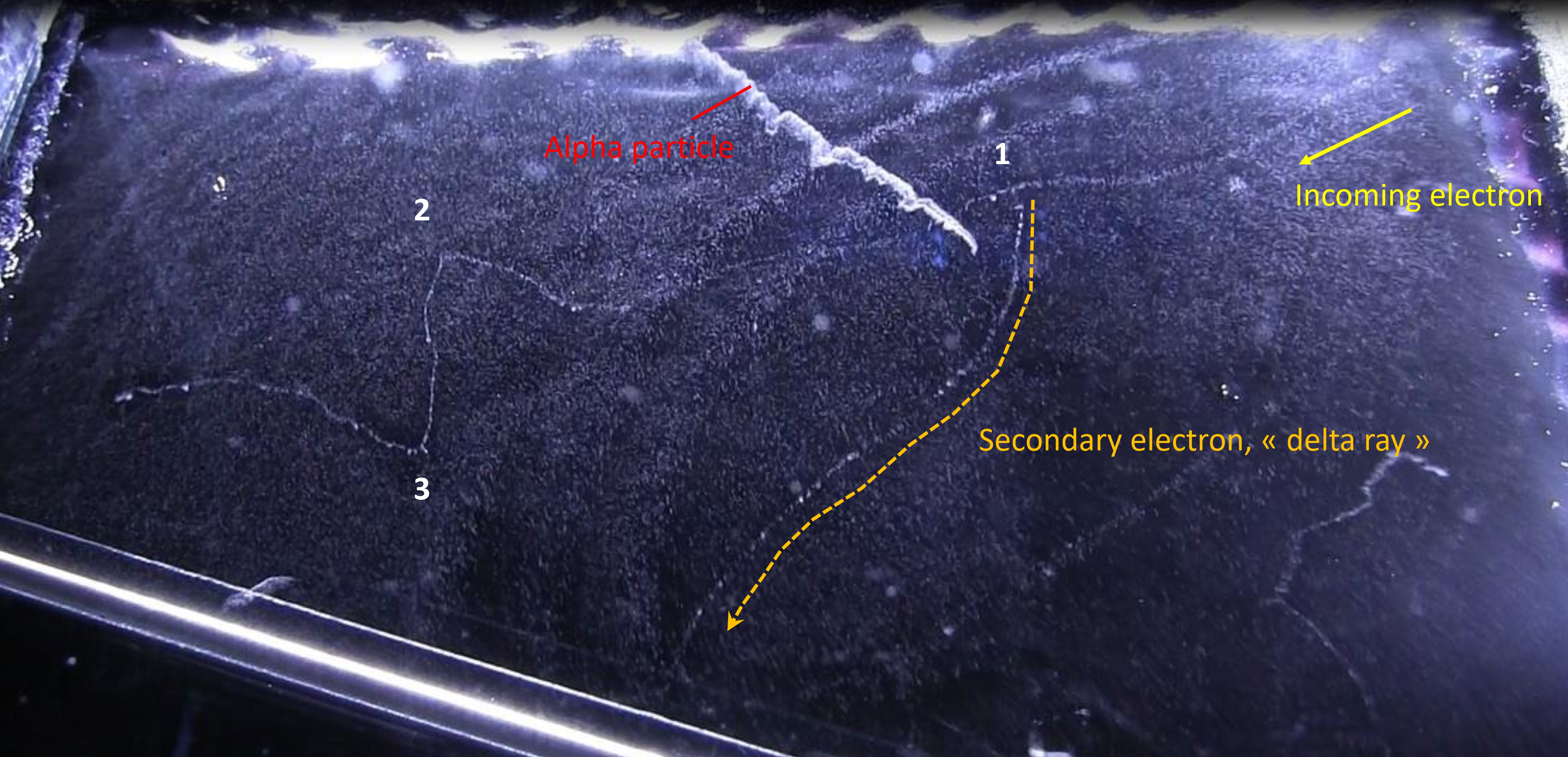
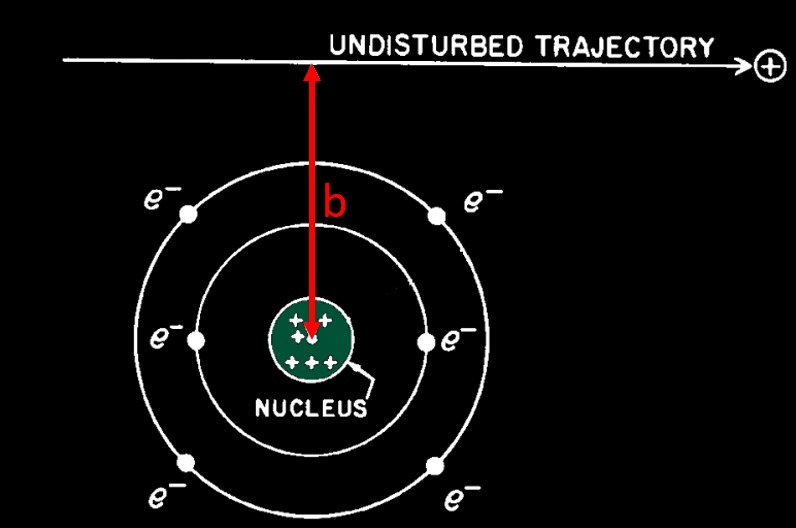
You can see the result of this energy loss in the next picture, with all the droplets making paths of particles travelling in the cloud chamber. The thin trails, composed of few droplets are electrons, whereas the fat brilliant trail in up-middle is made of much more droplets than the electrons. From the density of droplets (resulting in a track of high brightness ) we can say that it’s an alpha particle. So we can recognize which particle come in the chamber, just by looking at the density of tracks. The more ionization in matter => the more ions => the more energy loss of the incoming particle. As the energy loss trough the path of each particle (alpha, electron, proton…) is determined, we can identify it by looking at the quantity of droplets which is proportional to the brightness of the track.
Let’s analyse this picture further. An electron is coming from the up-right and travelling to left. Near the alpha track in up-middle of the picture, in point –1-, we see a second track going to the bottom of the picture. This track has been created by the incoming electron. In this point, the distance of closest approach of the incoming electron is of the order of atomic dimensions : it results in a ionization of the atom with the ejection of one of it’s electron cloud. This electron (called a « delta ray ») get enough kinetic energy from the incoming particle to travel a long distance in matter and thus make its own track in a cloud chamber.
In the left of the picture, we see that the incoming electron make abrupt deviations (at point 2 and 3). This time, the particle went closer to a nucleus (impact parameter b low) and undergone a huge deflection by the electrostatic field of this nucleus. During this deflection, the incoming particle losses a high amount of energy by emitting X-rays (Bremsstrahlung). We can’t see the radiation emitted in the cloud chamber because X-rays are not charged particles and thus can’t create ions (but we can see the indirect X-rays interaction, like the tritium experiment). With this picture, we can determine the probability of occurrence between the collision and radiative process. At point 2 and 3, the huge deflection of the incoming particle show that there was 2 radiative process. If we count the number of droplet created along the path of the incoming electron, we will find about thousands (in fact this is the number of ions created by the particle). So the collision process is thousands time more probable than the radiative one, the latter involving small impact parameter.
We will also answer to the question, looking at the picture, why are the tracks left by alpha particles brighter than an electron’s track (in other words, why alpha particle produce more ions in matter than electron). See this page for answer.
Experimental proof that low impact parameter are scarce
Projectile : alpha particles.
L’expérience de Rutherford (1909) peut montrer la prépondérance entre les deux processus de perte d’énergie pour une particule chargée traversant la matière. Dans une enceinte tirée au vide, il positionna une feuille d’or qui était bombardée par un faisceau de particule alpha collimaté. Les particules alpha provenant du Rn 222 ayant traversée la feuille étaient détectées spatialement avec un microscope muni d’un écran fluorescent en ZnS. Ainsi il pouvait mesurer l’angle de diffusion de la particule par rapport à sa trajectoire incidente.
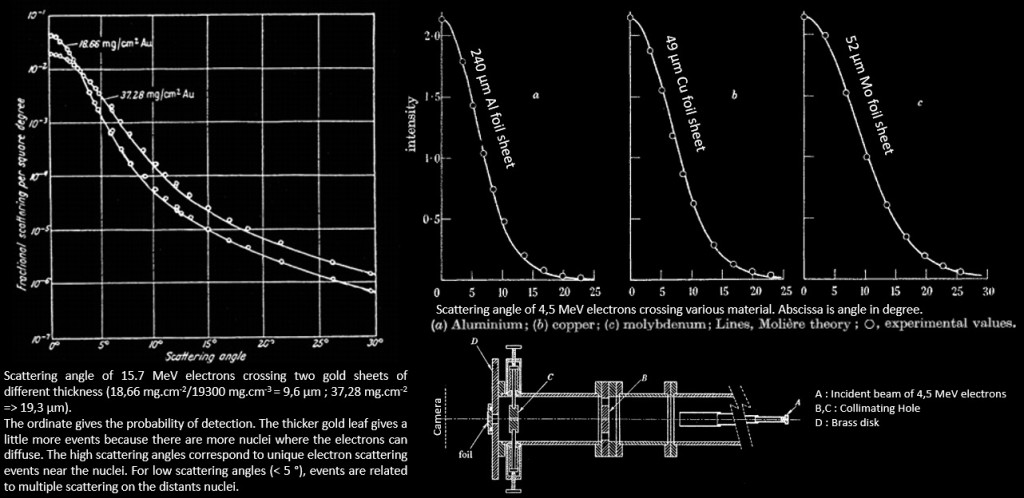
La courbe ci-dessous issue de l’expérience de Rutherford donne la probabilité de détection des particules alpha suivant l’angle de diffusion après que celles-ci aient traversées une feuille d’or de quelques μm d’épaisseur (ce qui correspond à une épaisseur de quelques milliers d’atome d’or). The α particle undergoes ∼104 interactions as a result of a foil thickness of 1 μm.
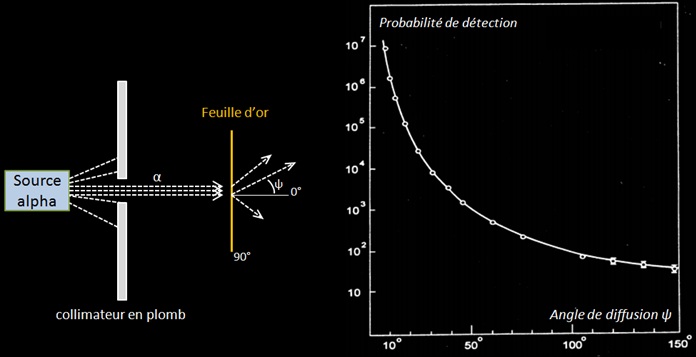
Expérience de Rutherford. La courbe montre la probabilité de détection (unité arbitraire) par rapport à l’angle de diffusion. Comme les particules alpha du Rn 222 ont une portée de quelques cm dans l’air l’expérience était réalisée dans le vide pour avoir un plus grand parcours des particules.
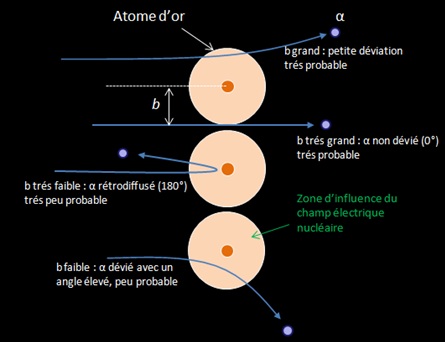
Geiger and Marsden found that more than 99 % of the α particles incident on the gold foil were scattered at angles less than 3° . They also found that one in ∼104 α particles was scattered with a scattering angle ψ exceeding 90° : « It was as incredible as if you fired a 15 inch shell at a piece of tissue paper and it came back at you ». Seul un champ électrostatique intense pouvait dévier une particule alpha aussi fortement, ce qui prouva que les atomes sont constitués d’un « noyau » où était localisée toute la charge électrique. Rutherford proposa le modèle nucléaire de l’atome en 1911 suite à ces observations.
La courbe et l’équation de Rutherford montrent que la diffusion des particules sur des noyaux se fait majoritairement sous de faible angles. Ces faibles angles correspondent à des paramètres d’impact élevés où la particule passe loin du noyau. En effet étant donné la structure lacunaire de la matière, un faisceau de particules alpha à beaucoup plus de chance de passer « loin » du noyau (b grand) que de passer près de celui-ci.
This experience show that interaction involving low impact parameter, and thus the radiative process, are scarce for alpha particles.
Projectile : electrons.
The same experiment can be made with electrons and the same result as heavy particle is obtained. The curves below coming from different article ( ex 1, ex 2, ex 3.) tell that small angle scattering is highly common, whereas large angle scattering is very rare. However, these are the result for the scattering of fast electron (several MeV). If they encounter more thickness of material, they will lose their energy and when its < 100 keV, large angle scattering will be more frequent (see the latter formula with ΔE).
Energy loss and scattering by collision process
We saw previously that low impact parameter involve radiative process, and that’s a relatively rare phenomenon versus the collision process. This latter process involve high impact parameter, that’s to say the charged particle traversing a material medium will pass far from a nucleus, but not too far from the atom. Matter is made of atoms, which is composed of electrons and nuclei. If a charged particle pass nearby an atom, it will transfer energy and momentum to the closer electron and nucleus. During this exchange, the charged particle will be scattered, or deflected of a very small quantity θ from it’s initial direction of travelling.
The aim of this topic is to identify what are the quantity of energy loss and angle of scattering undergone by the incoming particle, to an electron or a nucleus. To a first approximation, matter can be seen as a mixture of free electrons and nuclei at rest. The charged particle will feel the electromagnetic fields of the electrons and the nuclei and in this way undergo elastic collisions with these objects. The problem will be studied with 1 atom of oxygen (see next picture). But in a cloud chamber the volume is made of many atoms of different structure : H2O, O2, N2, alcohol molecule… and so the particle will interact multiple time with them.
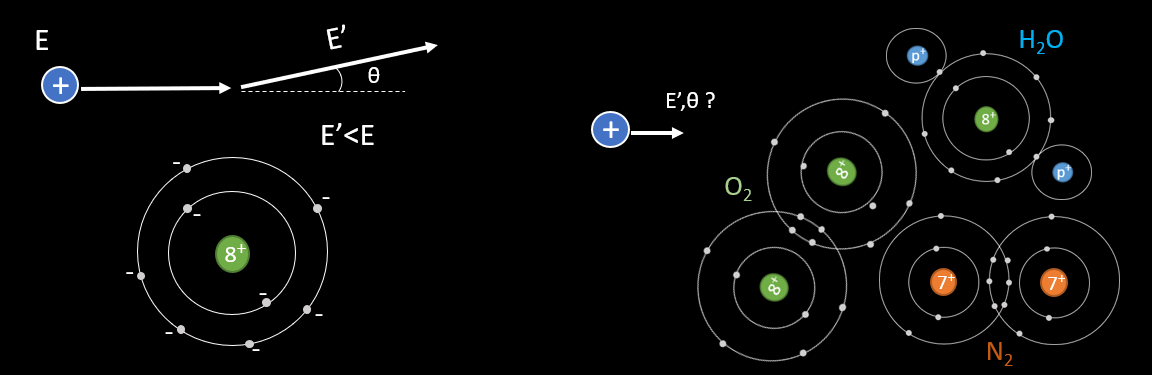
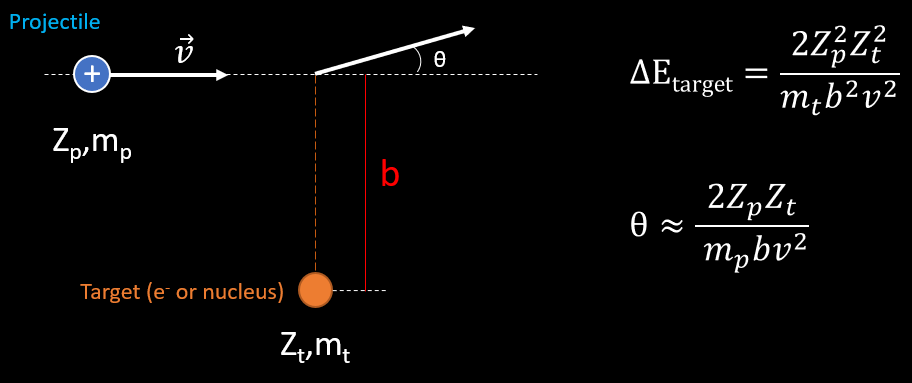
The problem can be studied in a simpler manner with application of electromagnetism (picture below). Consider that the projectile is a non relativist heavy particle with mass mp and charge Zp whose initial velocity in the laboratory reference frame is v. In this frame, the scattering material is at rest : it can be an atomic electron or a nucleus. We define the impact parameter b as the minimum traversal distance between the projectile’s initial direction of movement and the target position. The classical energy transfer to the atomic electron is defined with ΔE. The scattering angle of the projectile is θ.
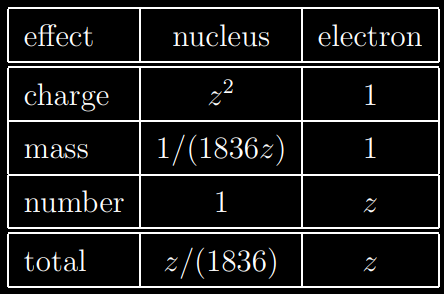 The energy transfer is proportional to the square of the charge of the target particle and inversely proportional to its mass. Possible targets are electrons and nuclei. A nucleus has a larger charge than an electron by a factor of the atomic number Z, giving the nucleus an « advantage » by a factor of Z2 when it comes to extracting energy from the incident particle. However, nuclei are more massive than electrons by a factor of 1836A where A is the atomic weight which is as large as or larger than Z (don’t forget the mass of neutrons). Furthermore, there are Z more electrons than nuclei to act as targets. Hence we see that the electrons are more effective than nuclei at taking the energy of the incident particle by a factor of at least 1836. For this reason, we shall henceforth keep in mind that most of energy is lost by the incoming particle to the electrons of atoms.
The energy transfer is proportional to the square of the charge of the target particle and inversely proportional to its mass. Possible targets are electrons and nuclei. A nucleus has a larger charge than an electron by a factor of the atomic number Z, giving the nucleus an « advantage » by a factor of Z2 when it comes to extracting energy from the incident particle. However, nuclei are more massive than electrons by a factor of 1836A where A is the atomic weight which is as large as or larger than Z (don’t forget the mass of neutrons). Furthermore, there are Z more electrons than nuclei to act as targets. Hence we see that the electrons are more effective than nuclei at taking the energy of the incident particle by a factor of at least 1836. For this reason, we shall henceforth keep in mind that most of energy is lost by the incoming particle to the electrons of atoms.
However, if we look at the scattering formula, things change. θ is directly proportional to the charge of the target if we consider the same value of b for one electron or nucleus as a target. If the target is an electron, Zt=e (e= elementary charge). If the target is a nucleus, θ ≈Ze. For example, if the nucleus is oxygen, the angle of scattering of the incoming particle will be 8 times than the angle of scattering induced by an electron. The angle of scattering is even smaller as the mass of the incoming particle is heavier. Thus, scattering of the projectile by atomic electrons can be neglected over the scattering induced by nuclei.
The next no-approximated formula of scattering is the probability that a charged particle of z,mp,v traversing a thickness of medium undergoes a collision which deflects the trajectory of the particle into the solid angle dw about θ from its original direction.
This formula (slightly simplified) tell that the probability of scattering at large angle is very small, but increase with the Z2 of the medium and z² of particle. If the particle is lighter and its velocity is low, the probability of scattering at large angle increase, but not at the same rate of the probability of scattering at small angles (factor of 1/θ4) . Thus, when a particle lose more and more energy by collision with atomic electrons, the particle is more and more scattered by nuclei as v decrease. The direction of motion of the particle continually changes as a result of frequent, small deviations due to Coulomb Scattering by the atomic nuclei near it’s line of motion. We call this the multiple scattering and the average angular deviation of a particle is approximately proportional to Z/pv (p is the momentum).
Note : multiple scattering correspond to the deviation of the path of a particle by the action of the electrostatic fields of nuclei. The effect of the Coulomb field of atomic electrons can be considered negligible over the total scattering of the particle. If we look at the equation of the scattering probability in the field of atomic electron we will see that their contribution to scattering is fairly small (10% for Z = 10, 1% for Z = 82) even if their collisions are responsible for almost all of the energy loss of the incoming particle.
We can illustrate the multiple scattering with theses pictures of an alpha source of 5 MeV traveling in different gas in a cloud chamber :
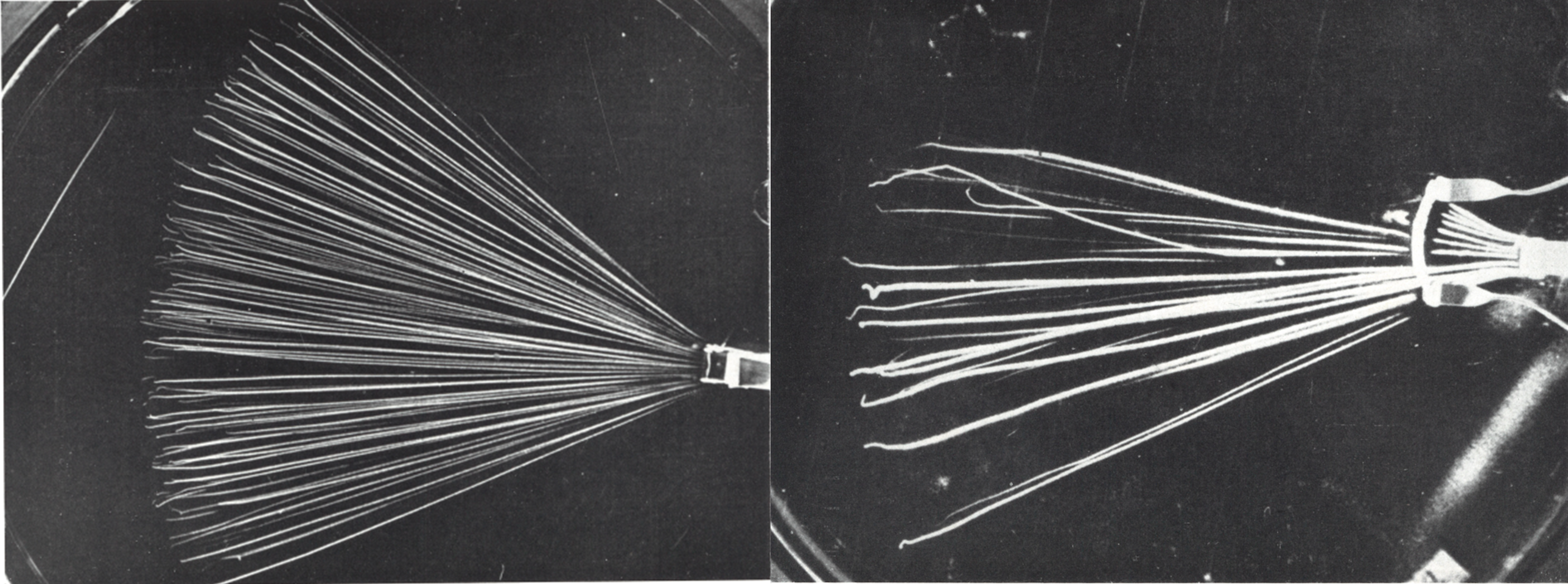
Left : Air + alcohol at a pressure of 18 cm Hg, average atomic weight A is 14 u : . Right : Xe gas + alcohol at 10 cm Hg, average atomic weight A is 131 u.
The above pictures show the passage of polonium α-rays through various gases. α-rays are slowed down mainly by interaction with the atomic electrons of the matter through which they pass. There is also interaction with the electric field of the atomic nuclei, causing mainly small deflections of the α-rays which as a whole result in a small irregular curvature of the tracks. The deflections show a strong increase with decreasing velocity of the α-rays. This increase is clearly seen in the photographs towards the end of the tracks. Furthermore, multiple scattering increases strongly with the atomic weight of the substance traversed. In the right picture with the heavy gas Xenon, deflections up to nearly 180° are seen. These large deflections are the result of a single large-angle scatter to a nucleus with a low impact parameter. Another example, when a muon is scattered in a nucleus from a photographic emulsion.
We said, especially looking to the gold foil experiment of Rutherford, that the probability that an incoming particle have a low impact parameter with a target is scarce. But it happen that we can see this type of event in a cloud chamber. So the next chapter below and to the end of this web page, (except the article talking about the radiative loss process) describe precisely what happen with a low impact parameter. Depending on the mass of the projectile and target, a lot of various scattering angles and energy transfer can be observed.
Energy transfer and angle in elastic scattering with non-head-on collision (b≠0)
De nombreuses interactions observées dans une chambre à brouillard peuvent être expliquées par une approche mécanique des collisions c’est-à-dire en négligeant les interactions à distance des particules entre elles (leurs charges deviennent nulle). Cela revient à traiter ces collisions d’une manière classique avec des chocs réel entre les particules où seules les masses et vitesses entrent en compte. Bien que cette approche soit éloignée de la réalité, elle permet d’estimer simplement les quantités d’énergies échangées lors des chocs entre particules. Dans ce qui suit on négligera les énergies de liaison des électrons aux atomes, la force électrique, et on considérera que la vitesse du projectile est non relativiste.
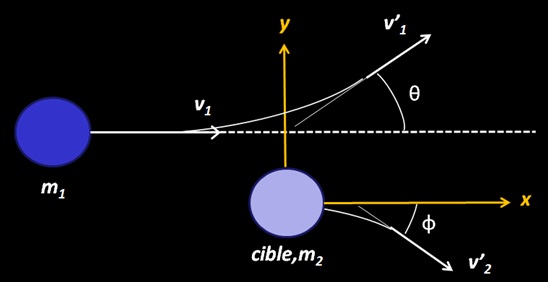
La collision à lieu entre un projectile de masse et de vitesse m1,v1 sur une cible immobile de masse m2. Il existe deux angles de diffusion : un angle θ pour le projectile et un angle Φ pour la cible. Le paramètre d’impact correspond à y ≠ 0 (la particule 1 percute la cible sur le bord)
L’énergie cinétique KE2 transférée du projectile à la cible se détermine à partir des lois de conservation de l’énergie cinétique et du momentum dont le détail figure ici. On obtient :
Où KE2 est l’énergie cinétique de la particule cible et KE1 l’énergie cinétique initiale de la particule projectile.
We have also: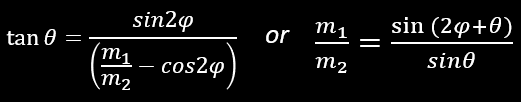
Angle of scattering from the values of m1 and m2 : A partir de l’équation précédente suivant la masse des entités en jeu nous pouvons identifier 3 cases of scattering.
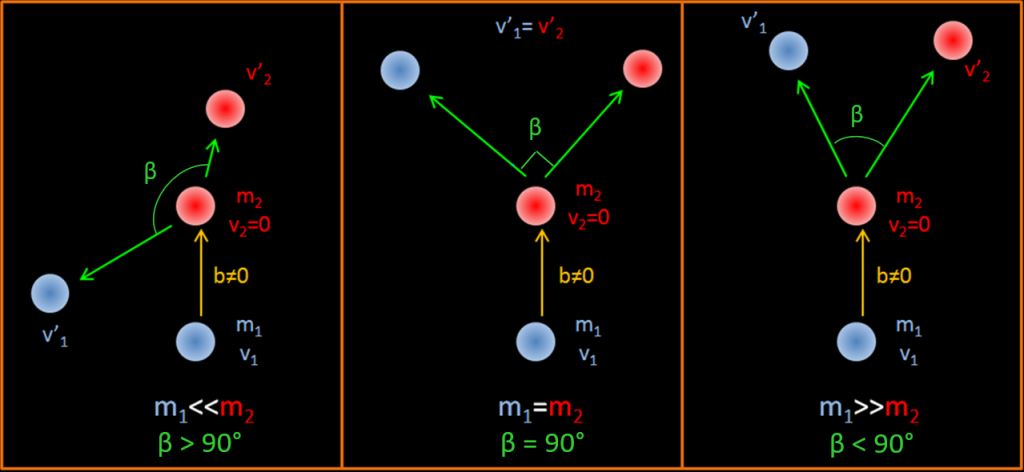
b≠0 signifie que la particule incidente percute la cible légèrement sur le bord et pas dans l’axe de la particule cible comme le montre le schéma.
We can observe this 3 cases in a cloud chamber :

Left (1932) : Alpha particle scattering in H2 gas in a 25 cm cloud chamber. A collision appear between an alpha and a H nucleus : case m1>m2. The particle going in right is the proton as it ionize less. Mid (1925) : Alpha particle scattering in Helium gas. A collision appear between an alpha and a He nucleus : case m1=m2. Right (1931): Alpha particle scattering in N2 gas. A collision appear between an alpha and a Nitrogen nucleus : case m1<m2.
Maximum energy transfer occurs when cos²Φ =1 , that’s to say b=0. This mean that the incoming particle make a « head-on » collision with the stationary particle.

Classic energy transfer relationship for a Head-on Collision.
After this type of collision if m1>m2 , θ = 0 and if m1<m2, θ=180° (the incoming particle bounce back on the stationary one. This is almost the case with the last right picture of an alpha scattering into a nitrogen nucleus, the angle β is 142°) . If m1=m2 the projectile stop on collision and the stationary particle move with the total kinetic energy of the first particle and with Φ=0.
The above equation is the classical result of the maximum energy transfer for a head-on collision between two particles. We will need later the relativistic form, introduced in this page. T’max mean KE2, the maximum energy received by the target m2 from the incoming projectile m1.
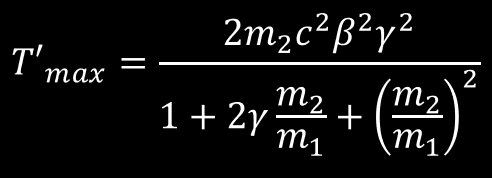
Relativistic energy transfer relationship for a Head-on Collision. Relativist quantity are defined here
Other examples of these 3 cases in a cloud chamber
m1 << m2
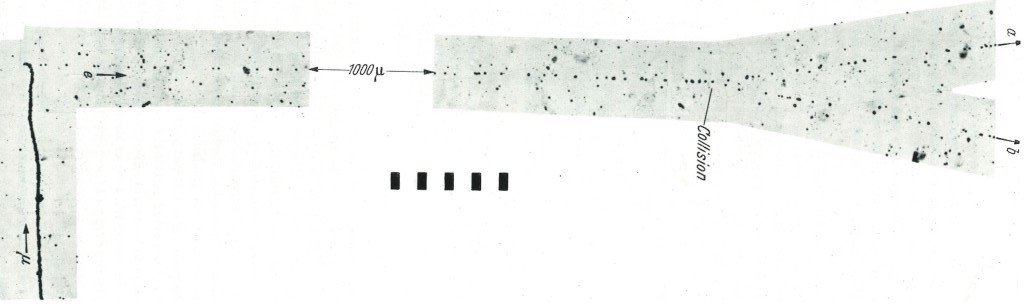
[Picture from 1936] An incoming electron (m1) coming from left, undergone a collision which scattered it at very large angle, almost 120° from its initial direction). This collision was due to a massive target, a nucleus (m2) under a small impact parameter. As the nucleus is massive (1836A time the electron), the electron didn’t transfer appreciable energy to the nucleus during the collision (refer to ΔE equation), but it lose a great quantity of energy by Bremssthralung. We can see that for m1<<m2, that the resulting angle of collision is higher than 90°. As the nucleus obtained no energy during the collision, we can’t see the recoiling nucleus.
There is a magnetic field about 300 Gauss in the chamber. Before the collision, the electron have to much energy to be deflected by this magnetic field. After collision, the electron have much less energy than before : it’s sensible to the magnetic field and thus start to make a spiral in the chamber. Near the end of its range, this electron undergo a second collision with a nucleus and is again deflected within a high angle, losing its last energy into Bremssthralung. Another case of collision of an electron on a nucleus.
What are the energy transfer in this collision ? This is not a « head-on » collision because the electron didn’t bounce back from the nucleus (θ would be 180° in this case or it’s about 120°). But let’s calculate what would be the maximum energy transfer if b=0. For example an electron (m1=0,511 MeV/c²) percutant un noyau d’hydrogène (m2=938 MeV/c²) :
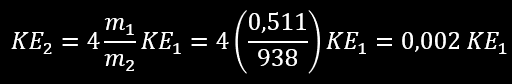
m1 term in denominator is negligible over m2
We see that in a direct hit between a moving electron on a proton, only about 0,2 % of the electron kinetic energy is transferred to the target proton in a single collision. The electron will also loose a considerable amount of energy by Bremsstrahlung during the collision (see latter in this page). Example 2 : α particle colliding with gold nucleus (Au-207), 4*4/196=0,08 we see that in a single direct hit head-on collision only about 8 % of the incident α-particle kinetic energy is transferred to the gold target. Example 3 : a neutron scatter into a lead material, 4*mn/mPb = 0,02*KE1, we see that in a direct hit only about 2 % of the incident neutron kinetic energy is transferred to the lead target. This shows that lead is a very inefficient material for slowing down the neutrons; low atomic number materials are much more suitable for this purpose. If you replace the lead with Boron, used in nuclear power plant as neutron moderator the energy transfer is 4*mn/mB =0,36*KE1(single hit goes to 36%). Lead is efficient to stop gamma rays (like high density material) but not neutron beam.

Left, a recoil nucleus in one of my cloud chamber. Alpha particles come from an Am 241 source. The air in the chamber is made of O,H,N and C nucleus. The angle between the 2 particles is a little more than 90°. This indicate that the alpha particle is lighter than the nucleus. The latter received enough energy from the alpha to « recoil » : during the collision, the nucleus lose temporally some of its electrons cloud, the nucleus (i.e the atom) is ionized. With the little kinetic energy received by the collision, the nucleus can displace in matter but not too far as the kinetic energy is low. In this picture, the track of the nucleus is about 1 mm. From approximation, we can bet this a nitrogen or oxygen recoiling nucleus.
m1 >> m2 (the « delta ray » production case)
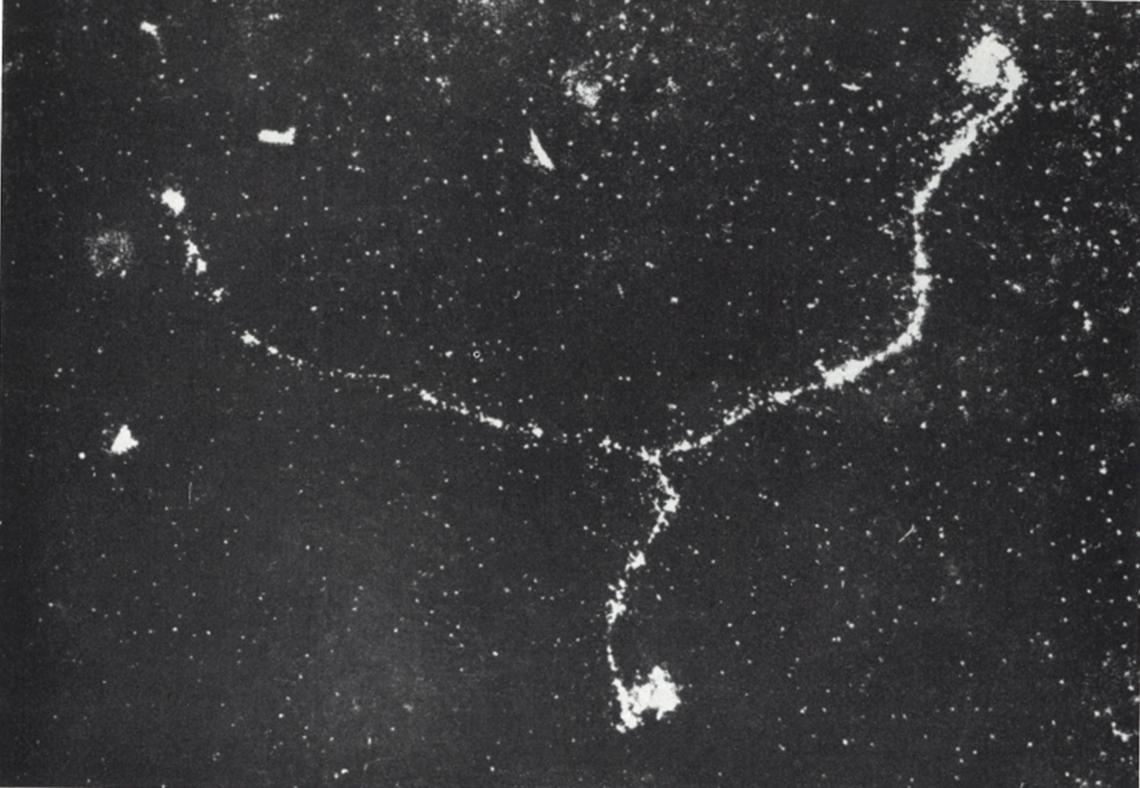
In the case of a collision of two equal rest mass particle (m0,1=m0,2 0 stand for « rest »), if one of them is at rest (m2=m0,2) and the other is moving at relativistic speed, m1=γm0,1. Thus, m1>>m2 and the subsequent direction of motion of the two particles is β<90°. Example below with a photographic emulsion of a muon (at left, moving upward) decaying into an electron. This electron moves right and have a kinetic energy about a dozen MeV from the μ decay process, its speed is relativist (See the graph, if the momentum of the incoming electron is about 40 MeV/c, is kinetic energy is 39,49 MeV so it’s speed 0,99991c) so its mass is not its rest mass, but a relativistic mass m1= γm0,1. A stationary electron (m2=m0,2) in the emulsion is then collisioned by the incident relativist electron. The angle θ between the 2 electrons is <90° because m1>>m2 even if they are the « same » particles.
The ejected electron is called a delta ray. Another example.
Again, what could be the energy transfer when a proton of KE1 scatter on an stationary atomic electron ? identical to the previous case (m1 << m2), the proton can give a maximum of 0,002*KE1 to the electron. Is it low for the electron ? no, as electron is a very light particle it can travel a good distance in matter with little kinetic energy. For example if the incoming proton have 10 MeV of KE1 the electron can get a maximum of 20 keV kinetic energy (in a b=0 collision) which allow him to travel about 8 mm in air. This distance is enough to see the electron track (the « delta ray ») in the cloud chamber. Proton of 10 MeV are common in sea level (natural background). Example of a delta ray in one of my cloud chamber :

From the length of middle delta ray (about 2 cm), the ejected electron have a kinetic energy of T’= 30 keV. To give this amount of kinetic energy to the electron, the proton should have at last KE1=15 MeV as previously stated. But to obtain 30 keV, the collision should have been « head-on » or the delta ray is produced « nearly » at an angle of θ=30° from the direction of proton. So T’max=T’/cos²θ which give T’max = 40 keV = KEelectron . Using KEelectron=0.002KE1, we get KE1 =20 MeV. This of course a very rough estimate of the kinetic energy of the proton. See this page about the angle of emission of delta rays.
In this case, both particles evolving in a collision have the same mass. To have a collision, this imply that one particle is moving, but not at relativistic speed so its mass is the same as its rest mass. This table indicate at which speed we can consider that a particle is relativist. For a 17 keV electron, γ (the lorentz factor) is 1,033. If this moving electron scatter into a immobile electron, we can say that m1≈m2 . This is not true at 80 keV, because γ = 1,15 thus m1=1,15 m2 . For a proton at 31 MeV , γ=1,033. At 145 MeV, γ = 1,15 and the proton is relativist.

Lorsque m1=m2,l’angle de séparation des particules après la collision est de 90°. On retrouve ce comportement dans les jeux de billard où les angles entre les boules après chaque choc (non frontaux, b≠0) sont proches de 90° (proche, car une partie de l’énergie est perdue dans les mouvements de rotation : les collisions ne sont pas parfaitement élastique).
We can observe this type of collision in a cloud chamber, if you are lucky enough when you study the natural background. Video of the event (picture in left) :
What you have recorded is a proton-proton elastic scatter . There is an interaction at the bottom of the picture by a cosmic ray proton with a nucleus in the walls of your chamber. This creates two visible protons entering your chamber. You can see that they are quite low energy protons (few MeV) because they are not perfectly straight lines. They are undergoing « multiple Coulomb scattering » with the air molecules inside your chamber (scattering off the atomic electrons). Because the protons are only a few MeV, these collisions can visibly deflect them. These collisions create the air ions that then act as the seeds for your cloud chamber droplets). One of the protons then collides with another proton – which either comes from a water molecule (one of its two hydrogen’s atoms), or, if you have an alcohol condensing vapor, one of the hydrogen atoms in the alcohol molecule. This second collision kicks the proton out of the water molecule and you now see both the scattered original proton and the new proton kicked out of the water molecule. The kinetic energy of the 2 emerging protons is equal to the incident proton’s kinetic energy, so the 2 emerging protons (in your case, which is almost symmetric about the incident direction) are each about one half of the incident energy. These last two protons are also seen to multiple coulomb scatter. Why do we know it’s p-p elastic scattering? The most striking signature is that the angle between the 2 emerging protons is 90 degrees (it appears a little bigger than 90 degrees because the tracks are pointing either a little towards your camera or away from it). Elastic scattering of two equal mass particles, where one is initially stationary, always gives an angle of 90 degrees between the two final particles. You can experimentally check this with a billiard table. Put a stationary ball at known position on the mid-line. Take a second ball on the mid-line and hit it towards the 1st ball at several different places. Measure the angle between the directions of the 2 balls after collision. You should find it is *always* 90 degrees (unless you do a perfect head-on shot!). Jasper Kirkby, particle physicist, head of CERN’s CLOUD experiment.
What are the energy transfer in the case m1=m2 ? In kinematic collisions, the maximum energy transfer to the projectile occurs when the masses are equal. We have to consider some special case, and to simplify, we will stay in a classical approach (the incoming particle have a reasonable velocity). The relativistic equation is here.
1. For b=0 (perfect head-on collision), between two distinguishable particles, the target will receive after the collision all of the kinetic energy of the projectile, so KE2=KE1 and the resulting angles of direction is 0. Example : positron (projectile with KE1) colliding with an orbital electron (target). The positron stop and the electron moves away with the kinetic energy of the incident positron. Note : for b=0 between two identical (indistinguishable) particles, we can’t say if the collision happened.

[Picture of 1951, b=0] : A 80 keV positron, coming from the left and moving to right (the direction of curvature is due to the magnetic field about 300 gauss in the chamber) collides with an atomic electron ; after the collision positron kinetic energy is about 5 keV (it form a local dense cloud of ionization). The electron move with almost all the kinetic energy of the positron and is deflected in an opposite direction by the magnetic field because its charge is negative. It’s not a perfect b=0 collision because the positron still have few kinetic energy after the collision.
2. For b≠0 (no head-on collision), between two indistinguishable particles, the target will receive after the collision half of the kinetic energy of the projectile, so KE2=0,5 KE1 and the angle β between the particles is 90°. Example : the proton-proton scattering event, billiard games, or electron-atomic electron . After the interaction, the particle with the larger kinetic energy is assumed to be the incident particle (in reality the target will receive a slightly less energy because the collision are not perfectly elastic ; some energy is wasted in excitation or radiative emission. ect…)
[Picture of 1935, b ≠0]. An electron of 56 keV of initial kinetic energy, coming from left and going to right, scatter on an atomic electron. As the primary electron have a no relativist velocity, its mass is same as an atomic electron so m1=m2. The resulting angle is 90° and each electrons have almost the same kinetic energy.
Energy loss by radiative process
Lorsqu’un électron se rapproche d’un noyau la force d’attraction Coulombienne F=Z1Z2/4πε0r² augmente et la particule est déviée de sa trajectoire suivant la valeur du paramètre d’impact. Lors de cette « collision » l’énergie du système et la quantité de mouvement doivent se conserver. Or la déviation seule de l’électron ne permet pas de conserver le momentum (on a p0≠p1 soit mv0≠mv1 car v0≠v1 il manque ainsi une quantité pour avoir p0=p1). L’électron au cours de son accélération (qui est une variation de sa vitesse, ici diminuant) émet un spectre de rayonnements X (des photons) pour rétablir la conservation de la quantité de mouvement totale (pphoton = hf/c où f est la fréquence du photon). Bremsstrahlung occurs when an electron is affected by the nucleus of an atom, scattered and then emits a photon. So there are three real particles involved: incident electron, scattered electron and emitted photon.
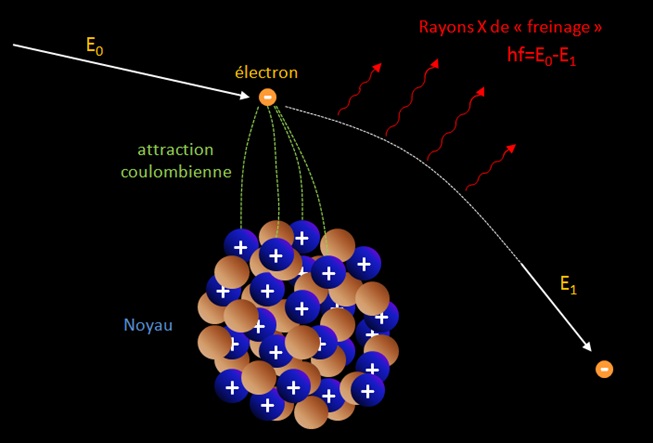
Note : the drawing is a false representation of the reality. When an electron of great energy produce a photon by bremsstrahlung, the angular divergence in the direction of motion of the two products may be very small of the order of mec²/E radians where E is the initial energy of the electron. For non-relativistic electron and photon energies the scattering angle tends to be mainly equally distributed, i.e. the photons do not have a preference for a particular direction.
La puissance rayonnée dE/dt par un particule chargée avec l’accélération a découle de la formule de Larmor :
Si l’on considère un électron s’approchant d’un noyau il est soumis à la force électrique et son accélération vaut :
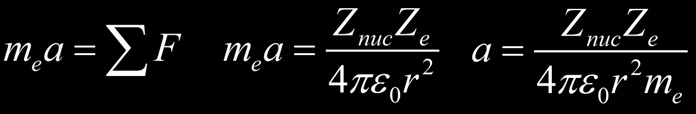
La puissance rayonnée par l’électron en rayonnement de freinage (Bremsstrahlung) est ainsi proportionnel à :
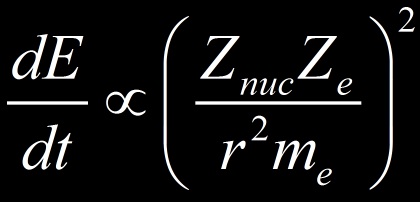
Nous avons considéré un électron me dévié par un noyau mais il pourrait s’agir de toutes autres particules chargées. D’après la formule on constate que :
- la perte par Bremsstrahlung est proportionnelle à la charge au carré des noyaux du milieu et de la charge de la particule (les tubes à rayons X utilise un faisceau d’électron avec une cible de noyaux lourd comme le Tungsten (Z=76) ).
- la perte par Bremsstrahlung est inversement proportionnel à la masse au carré de la particule (plus celle-ci est légère plus elle est susceptible de dévier et donc de rayonner).
- Plus la particule est proche d’un noyau (r), plus l’accélération est importante (ainsi que la déviation) et plus les pertes radiatives sont importante (dépendance en 1/r4)
Les particules lourdes seront peu soumises au rayonnement de freinage du fait de leur masse élevée : un muon est 207 fois plus lourd qu’un électron et perd ainsi 40.000 fois moins d’énergie par Bremsstrahlung qu’un électron. So radiative process are only for low mass particles such as electrons and positons.