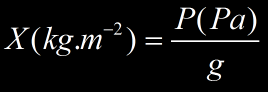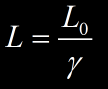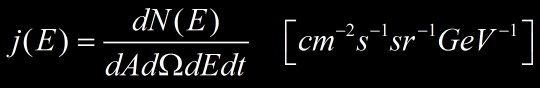Les paragraphes suivants décrivent pour les particules composant majoritairement le rayonnement cosmique au niveau de la mer, les flux et spectres en énergie.
Les muons μ
Peut t-on observer des muons dans la chambre à brouillard ? Oui… mais il faudra être patient !
Les muons représentent environ 70% du rayonnement cosmique chargé au niveau de la mer, le restant étant constitué d’électrons, et dans une très faible proportion par des proton et neutron (~2%). Cette prépondérance muonique n’est valable que pour un plan vertical, c’est à dire pour le rayonnement cosmique venant « d’en haut » sur nos têtes. Les chambres à brouillard ont une surface sensible perpendiculaire à cette direction, leur plan d’interaction est disposé horizontalement. Pour voir une particule, il faut qu’elle passe dans ce plan (90° par rapport à la verticale) à plus ou moins 1 ou 2 degrés, sous peine de voir la trace de la particule sortir de la zone de sensibilité.
Dans une direction horizontale, le flux muonique (nombre de muon traversant un détecteur par unité de surface et par seconde) ne représente qu’une fraction du flux vertical. La vidéo ci dessous montre un détecteur de muon en coïncidence . La détection en coïncidence permet d’écarter le bruit de fond parasite (électrons) en ne retenant au comptage que les particules passant simultanément entre deux compteurs espacés (ce qui est possible pour les muons étant donné qu’ils ne sont soumis qu’a une faible diffusion dans la matière du fait de leur masse élevée. Des électrons rapides peuvent cependant donner des signaux).
Dans la vidéo (au niveau de la mer), une flèche rouge apparaît lorsque un muon à traversé les détecteurs. Il y a 3 détecteurs sur la machine : un vertical, un horizontal, et un autre avec un angle de 45°.
La surface de chaque détecteur est de 250 cm². On constate qu’en une minute de comptage, bien peu de muon sont détectés dans un plan horizontal en dépit d’une surface de détection élevée ! Dans la chambre à brouillard, la surface sensible horizontale correspond au périmètre de la chambre multiplié par la hauteur de détection qui est représentée par l’épaisseur de la couche sursaturé sensible (+ la zone de drainage des ions par le champ électrique). On peut considérer que la surface sensible totale est de 48 cm². Par rapport à la vidéo ci dessus, on verrait donc 5 fois moins d’événements dans la chambre à brouillard.
Spectres des muons et flux
En 1932 Rossi à montré en utilisant des compteurs Geiger en coïncidence qu’environ 40% du rayonnement cosmique venant d’une direction vertical au niveau de la mer était capable de traverser 1 mètre de plomb. On pouvait scinder le rayonnement cosmique en deux composantes : une composante dure, capable de traverser au moins 15 cm (168 g/cm²) de plomb, et une composante molle qui est absorbée par la même épaisseur de plomb. On sait de nos jours que la composante molle est constituée d’électrons et de muons de basse énergie, tandis que la composante dure de muons (99%) et d’hadrons (n,p) de grande énergie. Les spectres et flux de rayonnement de cette page proviennent du livre de P.K.F Grieder « Cosmic Ray at Earth » contenant à peu prés 1000 pages de spectres sur le rayonnement cosmique, reproduit avec son aimable permission.
Production des muons
Les muons sont produits par la désintégration des pions et des kaons bien que ces derniers ne représentent qu’une faible contribution. Les pions et les kaons sont produits lors des interactions nucléaires avec les hadrons (primaire ou secondaire) avec les noyaux de l’atmosphère (voir le chapitre sur le rayonnement cosmique pour plus de détails).
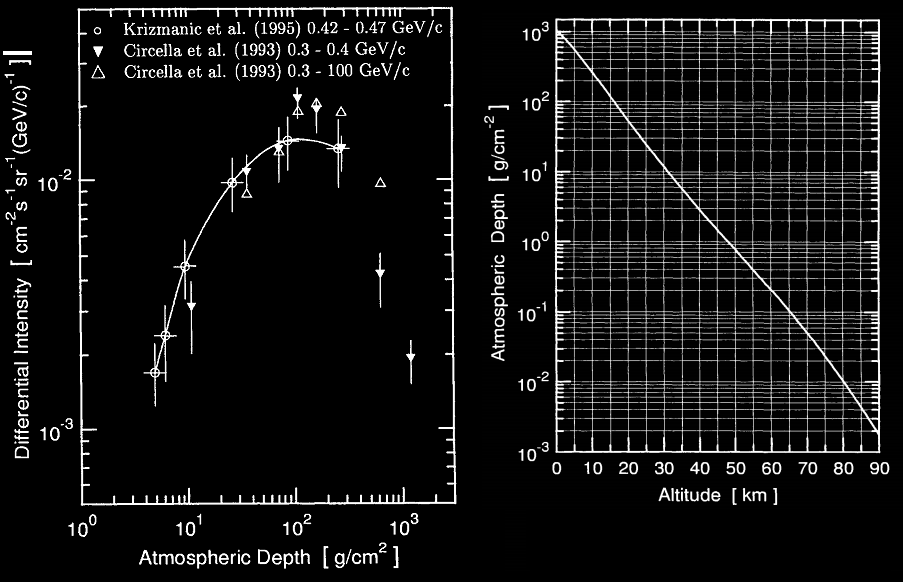
Flux muonique en fonction de l’altitude et correspondance entre la longueur d’interaction (g /cm²) et l’altitude. 3500 m correspond à 650 g/cm²
Le spectre ci-dessus, à gauche, montre la dépendance du flux muonique en fonction de l’altitude (la courbe de droite permet d’établir la correspondance g/cm² => km). Les résultats ont été obtenu par ballon sonde au Canada avec des spectromètres de masse embarqué. Les points en triangle vide couvre une large gamme de momentum [0,3-100 GeV/c]. Le flux muonique est maximal à une longueur d’interaction de 100 g/cm² ce qui correspond à une altitude de 15 km. On peut donc considérer que les muons prennent naissance à environ 15 km au dessus du niveau de la mer.
Les muons dissipent leurs énergies quasiment exclusivement par collision avec les électrons atomiques, les pertes radiatives n’étant présentes qu’a très hautes énergies. On a vu dans la page du dE/dx qu’une particule relativiste monochargée perd au minimum 2 MeV par cm2/g. Nous avons vu qu’il suffisait de multiplier cette valeur par la densité du matériau traversé en g/cm3 pour obtenir la perte d’énergie linéique en MeV/cm.
Les longueurs d’interaction en g/cm² prennent en compte la densité du matériau et sa longueur (g/cm3 * cm = g/cm2) et donnent des valeurs qui peuvent se comparer en elle. Exemple : 168 g/cm² correspond aussi bien à 15 cm de plomb où à 1,68 m d’eau. En multipliant la valeur de la longueur d’interaction par la valeur en MeV.cm2/g donné par la courbe de Bethe, on obtient directement la perte totale d’énergie collisionel dans le matériau traversé.
Le calcul de la longueur d’interaction pour l’atmosphère est un peu différent. La longueur d’interaction X (g/cm²) se calcule avec :
avec P la pression en Pascal (kg.m-1.s-2) et g la gravité (9,81 m.s-2). Diviser le résultat par 10 pour avoir une longueur d’interaction en g.cm-2.
A 12500 mètres d’altitude, la pression est de 18 kPa. La longueur d’interaction est donc de 180 g/cm² ce qui correspond à environ 15 cm de plomb. La densité de l’air à cette altitude vaut 3×10-4 g/cm3. La même longueur d’interaction de 180 g/cm² est obtenue pour une épaisseur d’air de 6000 mètres. Ainsi une particule perdra autant d’énergie par collision dans 15 cm de plomb qu’en traversant 6 km d’air à 3×10-4 g/cm3.
Au niveau de la mer, la pression est de 101325 Pa ce qui correspond à une longueur d’interaction de ≈1000 g/cm2. Par rapport à la densité de l’air au niveau de la mer (1,23×10-3 g/cm3), l’épaisseur d’air correspondante à cette longueur d’interaction est de 8 km. La densité de l’atmosphère diminue avec l’altitude (elle est 10 fois moindre à 15 km qu’au niveau de la mer). On peut donc considérer que les 8 km d’air précédent sont représentatif de ce que va réellement traverser un muon crée à 15 km d’altitude. Une particule relativiste perd au minimum 2 MeV par cm2/g ce qui représente une perte totale par ionisation de 2000 MeV pour un muon traversant l’atmosphère (1000 g/cm2). L’énergie moyenne des muons arrivant au sol étant d’environ 4 GeV, on peut estimer que les muons sont crées avec une énergie moyenne de 6 GeV.
Effet relativiste
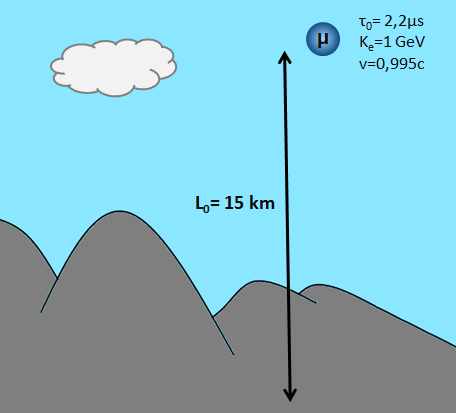 La demi-vie d’un muon dans son référentiel de repos est de τ0=2,2 μs. Si l’on considère qu’il est crée à 15 km d’altitude, aura t-il le temps d’atteindre le sol avant qu’il ne se désintègre ? Le schéma ci contre illustre le problème avec un muon à une vitesse v=0,995c , ce qui correspond à une énergie cinétique de 1 GeV (bien qu’a cette altitude l’énergie moyenne des muons est plutôt de 6 GeV).
La demi-vie d’un muon dans son référentiel de repos est de τ0=2,2 μs. Si l’on considère qu’il est crée à 15 km d’altitude, aura t-il le temps d’atteindre le sol avant qu’il ne se désintègre ? Le schéma ci contre illustre le problème avec un muon à une vitesse v=0,995c , ce qui correspond à une énergie cinétique de 1 GeV (bien qu’a cette altitude l’énergie moyenne des muons est plutôt de 6 GeV).
Le temps mis pour parcourir 15 km vaut :
t=L0/v=15000/3×108 = 50 μs =22,7 τ0 (on simplifie le calcul en posant v=c)
Le taux de survie des muons est donc de I/I0= e-t/τ0 =e-50/2,2=1,3×10-10 ou 1,3 muon qui arrive au sol pour une quantité initiale de 10 milliard, c’est-à-dire quasiment aucun.
Ce n’est pas ce que l’on constate en réalité car au niveau de la mer, les muons représentent la majorité du rayonnement cosmique (pour un flux de direction verticale). Les muons étant relativiste, il faut prendre en compte le facteur de Lorentz γ.
La demi-vie d’un muon dans son référentiel de repos est de τ0=2,2 μs mais dans le référentiel d’un observateur, la demi-vie du muon dépend de sa vitesse (comme de sa masse inertielle). On peut écrire que :
Le temps et la distance n’ont pas les mêmes significations par rapport à deux référentiels dont l’un est immobile. Dans le référentiel du muon, celui-ci voit que les distances se contractent à mesure qu’il accélère, tandis qu’un observateur au sol, voit « l’horloge du muon ralentir » mais aucun des deux ne voit les deux effets simultanément.
A une vitesse de v=0,995c , le facteur de Lorentz vaut γ =10 et la demi vie du muon, vu par l’observateur, est de 22 μs. Le nouveau taux de survie calculé indique que 10% des muons crée à 15 km d’altitude arrivent au sol. Cet effet relativiste à été vérifié expérimentalement par B.Rossi en 1940.
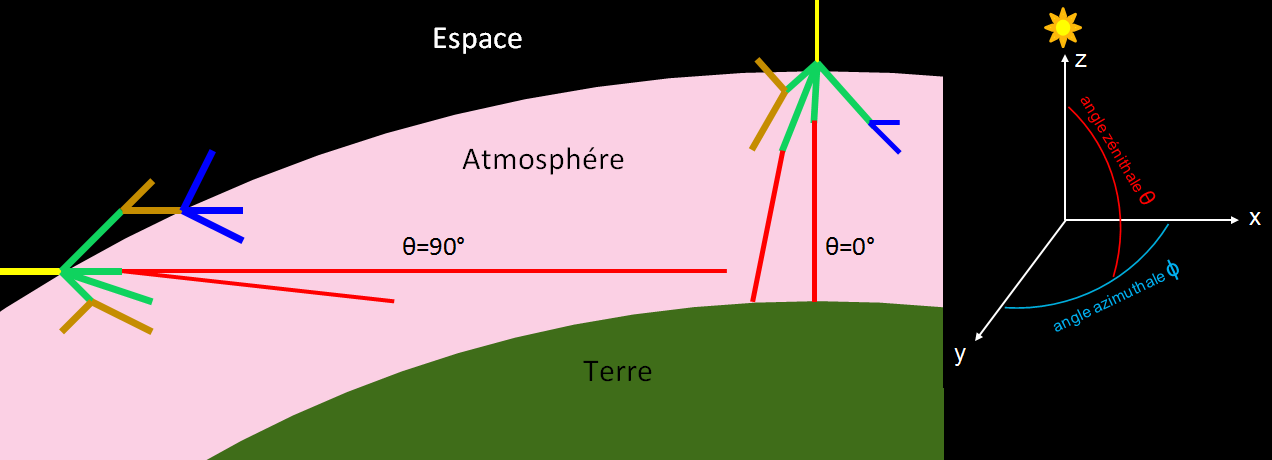
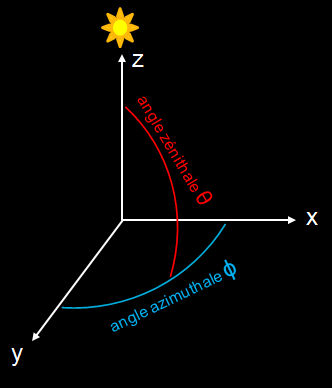
Dépendance du spectre par rapport à l’angle zénithale
L’intensité des muons détectés (nombre de muon par cm² par seconde) dépend de l’angle de détection qui est défini par l’angle zénithale θ (schéma ci-dessous).
La dépendance des flux avec l’angle zénithale s’écrit comme suit :
Où I(θ) est l’intensité à l’angle considéré, I(θ°) l’intensité du flux vertical et n un facteur dépendant de la longueur d’interaction de l’atmosphère et de l’énergie des muons. Quelques valeurs de n sont donnés dans le tableau ci-dessous.
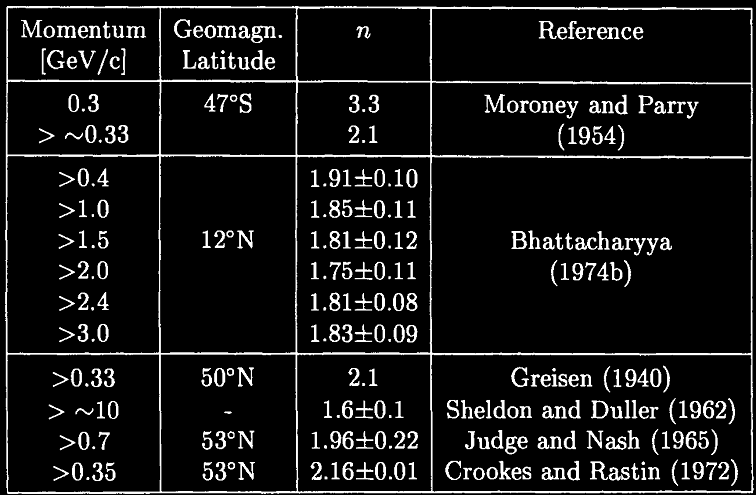
Valeur de l’exposant n au niveau de la mer (il convient de préciser que l’équation précédente au niveau de la mer est valable pour θ≤75°)
Un momentum minimum de 0,3 GeV/c est imposée : les muons au dessus de cette limite sont capables de traverser 168 g/cm² de plomb (composante dure).
L’exposant n à une valeur moyenne de 2 au niveau de la mer pour des muons de momentum minimum de 300 MeV/c. Si l’on considère un angle de 75°, cos²(75)=0,07 ce qui indique que l’intensité à 75° sera égale à 7% de la valeur de l’intensité verticale. En extrapolant pour des angles supérieurs, on constate que l’intensité horizontale sera encore plus faible. Ces différences s’expliquent par les longueurs d’interactions qui sont supérieure pour les muons arrivant à des angles élevés : ces derniers peuvent donc se désintégrer avant d’arriver dans le détecteur d’où une intensité très faible.
Une chambre à brouillard à diffusion ne pouvant fonctionner que dans un plan horizontale, (angle zénithal = 90°), on peut donc s’attendre à ce que le flux de muons traversant la chambre soit très faible, comme nous allons le voir par la suite.
.
.
.
.
Flux muonique à 3000 m d’altitude
Ces spectres peuvent être utiles lors de mesures au Pic du Midi (2900 m).
Spectre vertical
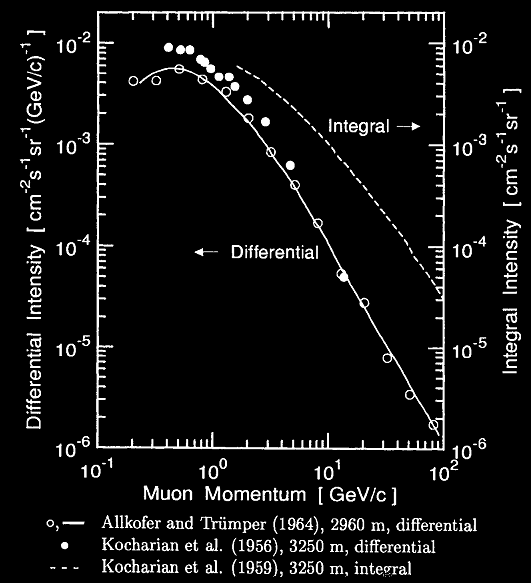
Spectre vertical différentiel en fonction des momentum de muons (positif et négatif) à une altitude de 2960 m (Zugspitze, Allemagne) et à 3250 m (Mt. Aragats, Armenie) avec son spectre intégral.
Le spectre différentiel j(E) est défini par le nombre de particules dN(E) par unité de surface dA, par unité de temps dt par unité d’angle solide dΩ, par intervalle d’énergie dE :
Ou autrement dit, le nombre de particule par cm² par seconde par steradian et par tranche d’énergie de 1 GeV.
Sur le spectre ci-dessus, par exemple pour une hauteur de 2960 m, l’intensité est maximale pour un momentum de 0,5 GeV/c et vaut 6×10-3 cm-2s-1sr-1(GeV/c)-1 .
Le spectre intégral j(≥E) s’obtient en intégrant le spectre différentiel sur les bornes [E ;+∞] :
Sur le spectre ci-dessus, pour des muons de momentum supérieur à 1 GeV/c l’intensité absolu vertical vaut :
Iv (≥1 GeV/c) = 6 x 10-3 cm-2s-1sr-1
Spectre horizontale (θ=84°)
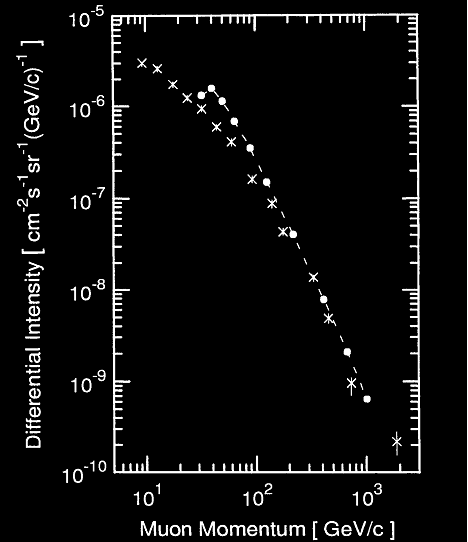
Spectre différentiel de muons (négatif et positif) obtenu avec un spectrométre magnétique sur le mont Aragats, Arménie (3250 m, 670 g.cm-2) pour un angle zénithale moyen de 84°. Les différents points proviennent de données réalisés en 1975 ou 1983 par les mêmes auteurs.
L’intensité la plus grande est obtenue pour un momentum de 10 GeV/c. Cela correspond à une intensité de 3×10-6 cm-2s-1sr-1(GeV/c-1).
Conclusion entre les spectres verticaux et horizontaux
Il est plus pratique d’utiliser des intensités intégrale couvrant toute les énergies afin de comparer les différences de flux à θ=0 ou 90°. Deux auteurs (Shen & Chiang, 1979) ont utilisés un spectromètre de masse pour déterminer les intensités à 3220 m dans un plan vertical Iv et horizontale Ih (angle zénithal moyen : 86,2°) :
Iv (≥2 GeV) = (4,9 ±0,2) x 10-3 cm-2s-1sr-1
Ih (≥2 GeV) = (9,68 ±0,32) x 10-5 cm-2s-1sr-1
A cette altitude, le flux horizontal est 50 fois moins intense que le flux vertical. La dépendance des flux avec l’angle zénithal se fait avec Ih =Iv cosn(θ) avec n=1,5.
Flux muonique au niveau de la mer
Spectre vertical
Quelques auteurs cités par P.Grieder :
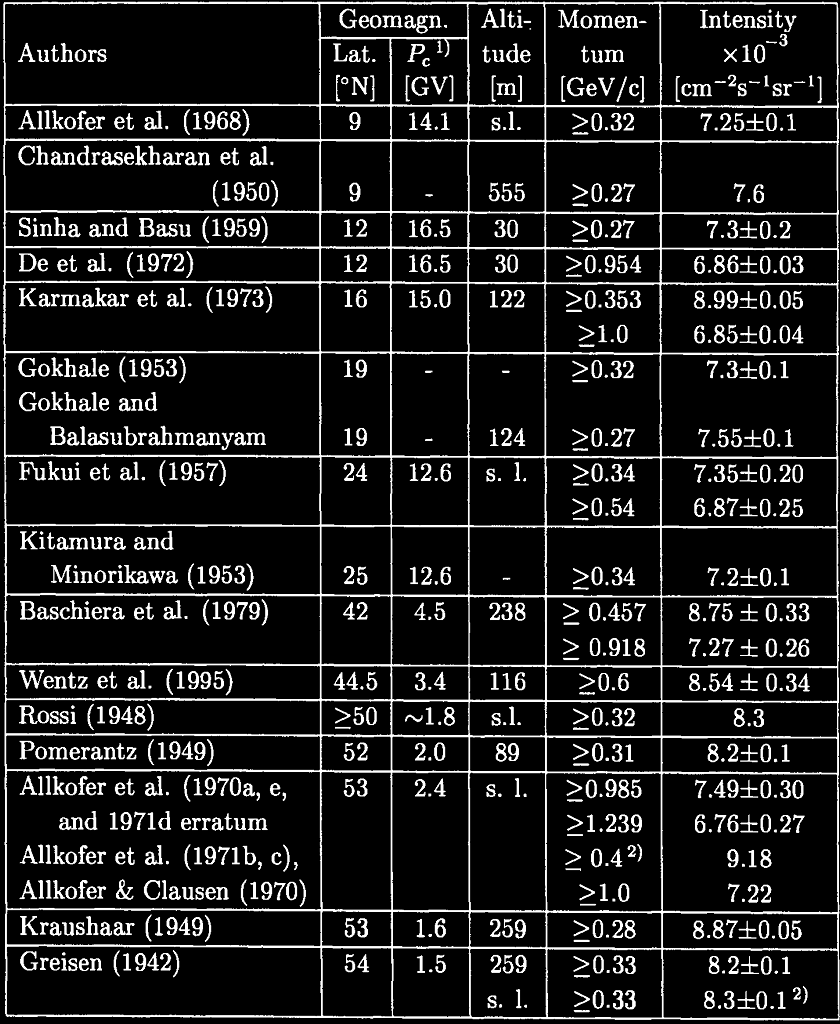
Intensités (intégrale) verticale des muons près du niveau de la mer pour la composante dure du rayonnement cosmique
Suivant un plan vertical, on peut retenir que l’intensité vaut en moyenne :
Iv (≥0,3 GeV/c) = 8 x 10-3 cm-2s-1sr-1
D’après cette valeur, on reçoit 0,48 muons par minute au niveau de la mer sous un angle θ=0°.
Si l’on prend en compte tout les muons venant de toutes les directions, c’est à dire avec un angle zénithal variant de 0 à π et un angle azimuthale variant de 0 à 2 π, P.Grieder cite une valeur effectuée en 1970 à une altitude de 259 m (Ithaca, NY) :
Jomni (≥0,35 GeV/c) = (1,9±0,12) x 10-2 cm-2s-1
Soit 1,14 muon par cm² par minute au niveau de la mer, ce qui équivaut à la taille d’un ongle.
.
.
Spectre vertical et horizontal
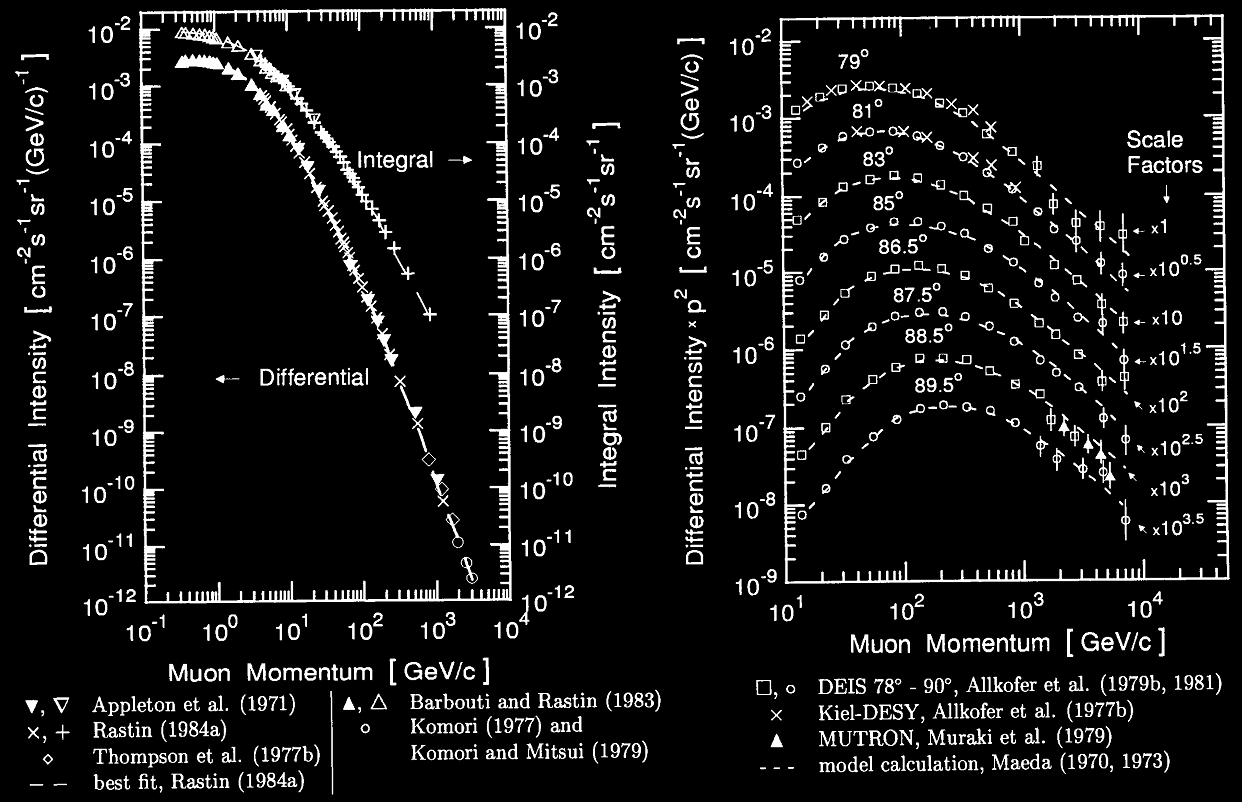
A gauche : Spectre intégrale et différentiel au niveau de la mer et pour un plan vertical.
A droite : spectre différentiel horizontale (78°-90°) au niveau la mer. Diviser l’ordonnée par le momentum au carré, et multiplier l’ordonnée par le facteur d’échelle pour obtenir la vrai intensité.
Spectre vertical : pour un momentum supérieur à 0,3 GeV/c, on retrouve sur le spectre intégral la valeur Iv (≥0,3 GeV/c) = 8 x 10-3 cm-2s-1sr-1 citée précédemment. Le flux est maximale pour un momentum de 1 GeV/c. En prenant en compte toutes les énergies, l’énergie moyenne des muons arrivant au sol est de 4 GeV.
Spectre horizontal : à 89,5° le flux est le plus intense pour un momentum de 200 GeV/c. L’intensité vaut :
Ih= 103,5 x 2 x 10-7 cm-2s-1sr-1 GeV/c /(200² GeV²/c²) = 1,58 x 10-8 cm-2s-1sr-1 (GeV/c)-1.
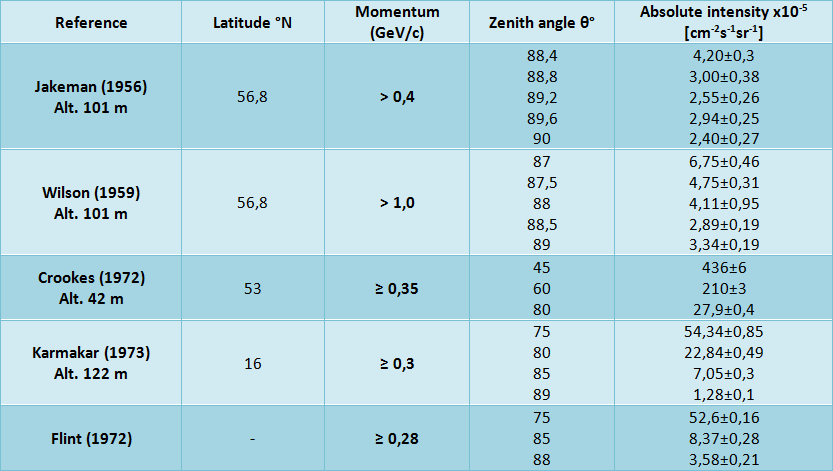
Pour le flux intégral horizontal, le tableau suivant cite quelques auteurs :
Suivant un plan horizontal (pour θ proche de 90°) au niveau de la mer, on peut retenir que l’intensité absolue vaut en moyenne :
Ih (≥0,3 GeV/c) = 2,65 x 10-5 cm-2s-1sr-1
Le flux muonique horizontal est 300 fois moins intense que le flux muonique vertical au niveau de la mer.
.
Des muons sous terre…
En arrivant au niveau de la mer, les muons les plus énergétiques (plusieurs dizaines de GeV) sont capables de traverser le sol, l’eau ou la glace qu’ils rencontrent. A ces énergies, les pertes radiatives sont importantes et le seront d’autant plus que le matériau est dense. En Inde, la mine de Kolar est profonde de 3200 m. Dans cette mine, à 270 m de profondeur, l’intensité absolue verticale est de 2,51 x 10-6 cm-2s-1sr-1. A 600 m l’intensité vaut 1,77 x 10-7 cm-2s-1sr-1 et à 2110 m 1,92 x 10-10 cm-2s-1sr-1.
… et dans la chambre à brouillard ?
Les chambres à brouillard à diffusion ne peuvent fonctionner que dans un plan horizontal, la gravité permettant la création de la couche sursaturée juste au dessus de la plaque froide. L’intensité intégrale muonique à p ≥ 0,3 GeV/c suivant un plan horizontal au niveau de la mer est de :
Ih (≥0,3 GeV/c) = 2,65 x 10-5 cm-2s-1sr-1
Pour les muons de basse énergie en dessous de 300 MeV/c (ce qui équivaut à Ke= 215 MeV), le spectre n’est pas connu mais des courbes complémentaires indiquent que les flux sont très faibles voir inexistant. A cette énergie, la portée dans l’air est de 740 m ou 36 cm dans l’aluminium (densité quasi identique à du béton). Ces derniers seront aisément absorbés dans les parois de bâtiments avant d’atteindre une chambre à brouillard.
Le périmètre de la chambre à brouillard est de 48 cm. La hauteur sensible de la chambre peut s’estimer à 1 cm avec l’influence du champ électrique drainant les ions dans la couche sursaturée (quelques mm d’épaisseurs). La chambre à brouillard est donc un détecteur avec une surface de détection de 48 cm². Le nombre probable de muon qui traverserait la chambre par minute serait de Ih x 60 x 48 = 0,076 min-1 soit 1 muon toute les 13 minutes.
Dans une chambre avec une surface sensible de 45×45 cm, le nombre de muon probable serait de 1 muon toutes les 3 min 30 au niveau de la mer. A 3000 m d’altitude, on observerait un muon par minute. La détection de muon avec des chambres à brouillard à diffusion est donc difficile au niveau de la mer : l’étude du rayonnement cosmique revient aux chambres à expansions qui peuvent fonctionner suivant des plans verticaux.
.
Les Hadrons n,p,π
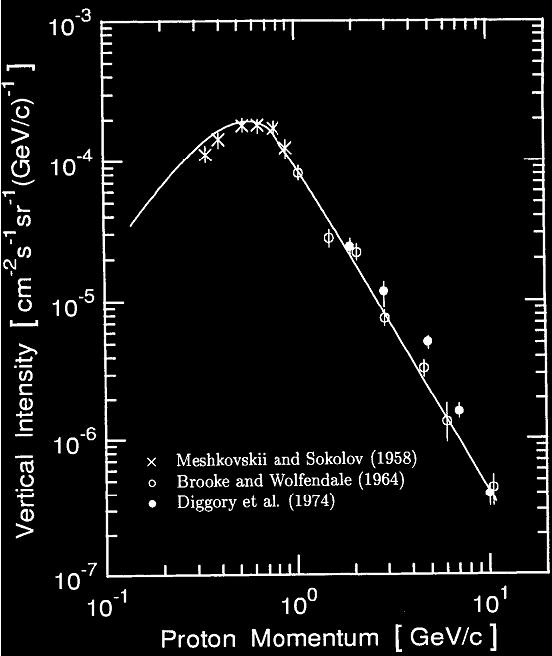
Flux de Protons au niveau de la mer
Remember you can transform the momentum in GeV/c into kinetic energy with this excel sheet. 1 GeV/c is about 433 MeV for a proton.
Le flux vertical est le plus intense pour un momentum de 600 MeV/c (soit une énergie cinétique de 175 MeV)
Iv= 2 x 10-4 cm-2s-1sr-1 (GeV/c)-1
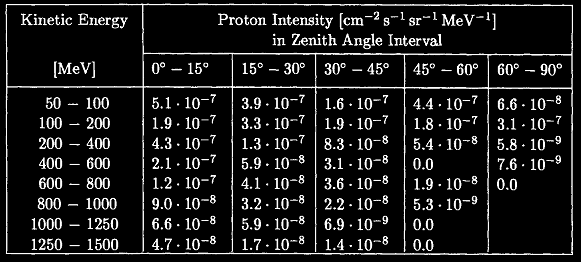
Très peu de valeurs sont disponible pour le flux horizontal, néanmoins P.Grieder cite Flückiger (1977) :
Dans l’intervalle [60-90°] le flux différentiel est maximum entre 100 et 200 MeV avec Ih= 3,1 x10-4 cm-2s-1sr-1 (GeV)-1
Avec ces valeurs [60-90°], l’intensité absolue horizontale calculée est de Ih (≥50 MeV) = 3,7 x 10-5 cm-2s-1sr-1 (une autre série de valeur donne 1,27 x 10-5 cm-2s-1sr-1).
Dans l’intervalle [0-15°], l’intensité absolue verticale calculée est de Iv (≥50 MeV) = 3,2 x 10-4 cm-2s-1sr-1
Flux de Protons à 3200 m d’altitude
P.Grieder cite Kocharian (1955) : Iv (≥80 MeV) = (1,69±0,02) x 10-3 cm-2s-1sr-1
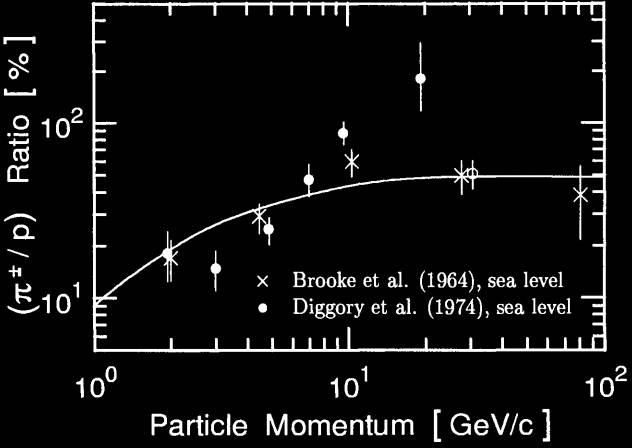
Flux de Pions au niveau de la mer
Bien que la demi-vie des pions soit très faible (2,6 x 10-8 s), ils peuvent être créer localement lors des interactions nucléaire par des hadrons (neutron, proton) sur des noyaux ou par réaction photonucléaire muonique. On peut donc en observer au niveau de la mer (bien que cela soit peu probable étant donné la taille de notre détecteur) :
Pour un momentum de 1 Gev/c, il y a environ 10 fois moins de pion que de proton (la proportion de pion augmente avec l’énergie).
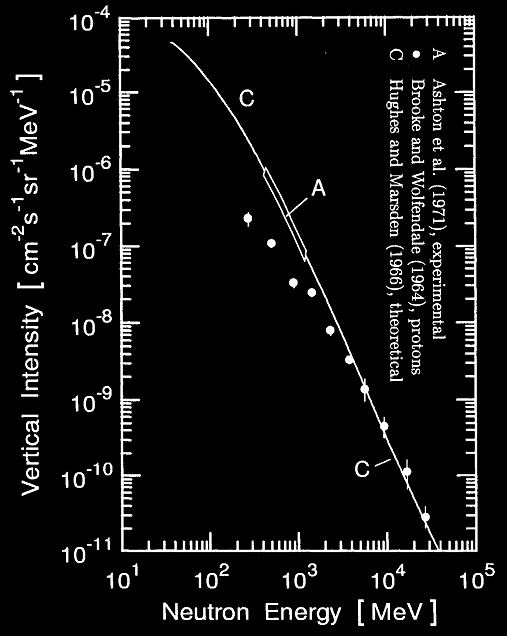
Flux de Neutron au niveau de la mer
Le flux est sensiblement identique à celui des protons pour E> 1 GeV.
L’intensité omnidirectionnelle à été mesuré par Hajnal (1971) et vaut Jomni = 8,2 x 10-3 cm-2s-1 , proche de celui des muons.
En altitude (~3000 m), l’intensité verticale vaut Iv (50<E<350 MeV) = 2 x 10-3 cm-2s-1sr-1.
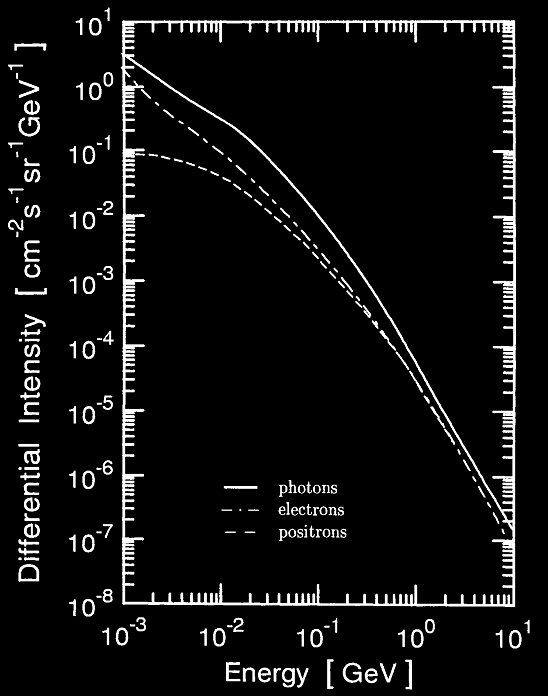
Photons et leptons e–,e+
Au niveau de la mer pour une composante verticale le flux de photon et des électrons (Daniel and Stephens, 1974) :
Pour E> 100 MeV le ratio photon/électron est proche de l’unité. On a l’intensité intégrale verticale pour les photons au niveau de la mer :
Iv (≥100 MeV) = 10-3 cm-2s-1sr-1
En altitude (~3000 m), Iv (≥30 MeV) = 10-2 cm-2s-1sr-1
Pour les leptons, Greisen (1942) ont mesurés au niveau de la mer l’intensité intégrale verticale :
Iv (≥10 MeV*)= 3,1 x 10-3 cm-2s-1sr-1
*Les bornes de l’intégrale précédente ne sont pas connu mais d’après le National Physical Laboratory une énergie de coupure à 10 MeV semble cohérente.A 3600 m pour les leptons, Wibberenz (1968) : Iv (≥100 MeV) = 8,8 x 10-4 cm-2s-1sr-1
Le flux muonique vertical au niveau de la mer est de 8 x 10-3 cm-2s-1sr-1. De manière générale on considère que le flux électronique au niveau de la mer vaut 35 à 40 % celui des muons.
.
Résumé
Au niveau de la mer les différentes composantes verticale du rayonnement cosmique ont les proportions suivantes :
At sea level, for every 10,000 muons, there will still be roughly: 200 primaries (protons and occasional neutrons), 20 high-energy electrons (E>1GeV), and 4 pions. But there may be up to 100,000 low energy electrons created by the cascade. These particles are absorbed quickly, but if the shower is energetic enough or the shower started low enough, they may still be the most prevalent particles at sea level.
A environ 3000 m d’altitude la composante hadronique s’intensifie :
Pour les flux horizontaux les données sont trop disparate pour pouvoir en faire une synthèse.