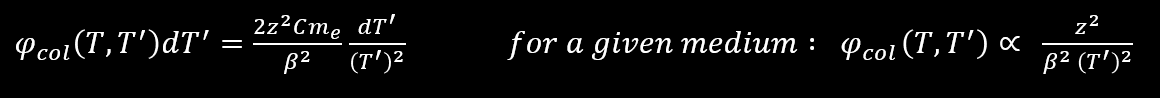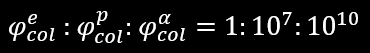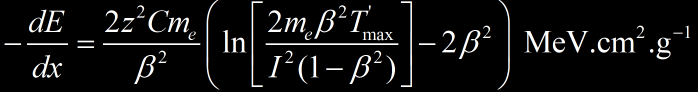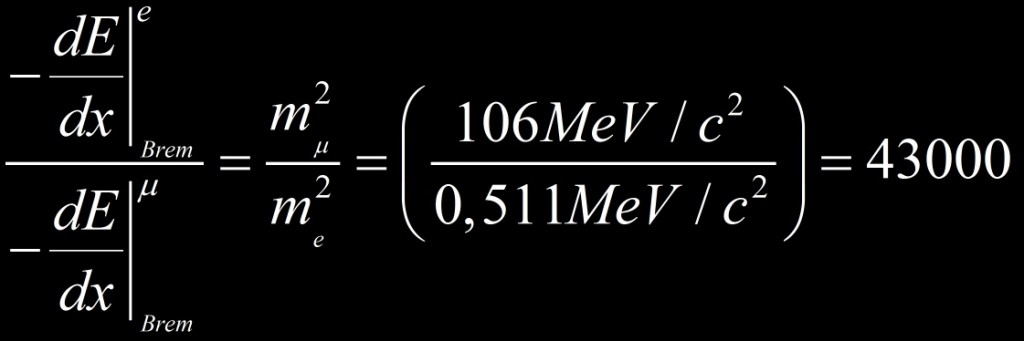Looking at the picture below, why are the tracks left by alpha particles brighter than an electron’s track (in other words, why alpha particles produce more ions in matter than electrons).

Picture taken in 2012 at 2877 m height in France (Pic du Midi) in a PJ45 cloud chamber. The length of this picture is about 40 cm. Looking at the brightness of each track, we can tell which particle entered in the chamber.
Previously we said that charged particles lose their energy mostly by interactions with the atomic electrons. Interaction mean « excitation or ionisation » of atoms which involve a loss of energy of the incoming particle. The amount of energy transferred to an atomic electron was defined with ΔE. Charged particle encounter also nuclei, but in these electrostatics collisions the incoming particle don’t lose much of energy, it’s only deflected from it’s trajectory (this is the « multiple scattering » which increase as velocity decrease). Sometimes, a charged particle come close enough to a nucleus and then it can lose a substantial quantity of energy depending on the mass involved between the projectile and target, but this a rather rare process like Rutherford showed with the gold foil experiment.
To resume, charged particle lose their energy « only » with atomic electrons according to the quantity ΔE. But this quantity was defined with only one target (one atomic electron). There is never just one electron in matter. So how often a particle lose energy in matter ?
The formulas below give the collision probabilities with atomic electrons (which are called delta ray, that’s to say that the atomic electron obtain at last 100 eV of energy during the collision to make is own track).
The differential collision probability φcol(T, T’)dT’dx is defined as the probability for a charged particle of kinetic energy T, traversing a thickness dx(g/cm2), to transfer an energy dT’ about T’ to an atomic electron (assumed free that’s to say the binding energy to atom is neglected). These formula consider that T >> mec2 (>>0,511 MeV) :
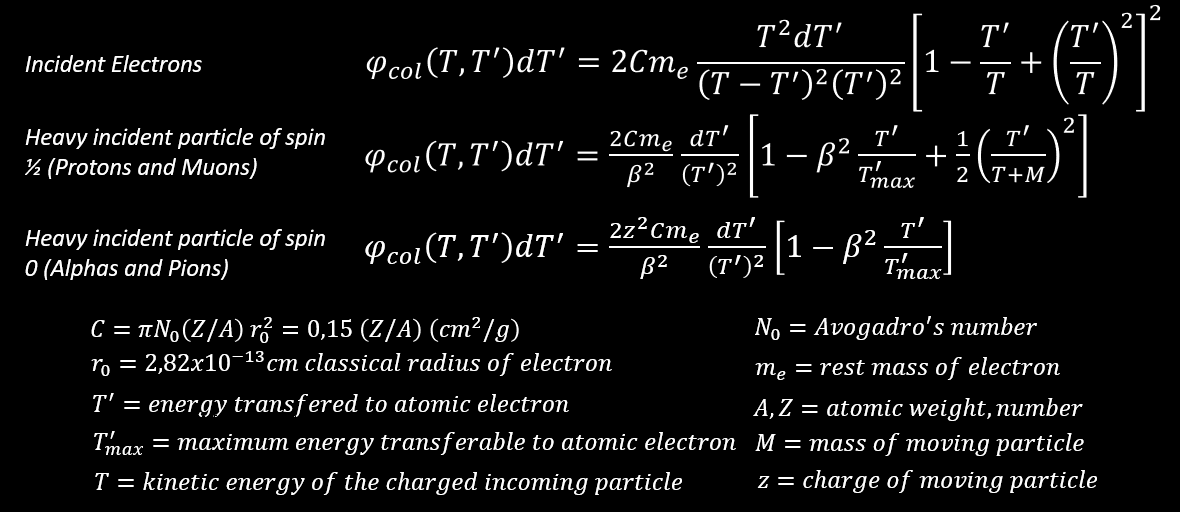
For the last formula about particles of spin 0 like alpha, we have to multiply by z²=4 as the alpha particle is charged twice (other formulas consider z =1, z is the charge of moving particle).
The dependence of φcol come from 3 mains factor : The factor C expresses the proportionality of the collision probability to the electron density of the medium. The factor β-2 expresses the dependence of the energy transfer on the collision time. The factor T’2 expresses the fact that collisions with large impact parameters are more likely than collisions with small impact parameters. For this latter, we can consider an approximated case where T’ << T’max (i.e distants collisions with little energy transfer). This simplification is a good approximation of the reality as experiences showed us that large impact parameter b is much more probable than low one inducing high energy transfer. The all above formula becomes :
Consequently the probability of a collision of the incoming particle with an atomic electron is higher for a slow particle transferring small amounts of energy T’ in each collision. And this probability increase with the z² of the particle.
What is T’max for an incoming heavy particle or an electron ? The maximum energy transfer that can be given to an atomic electrons is :
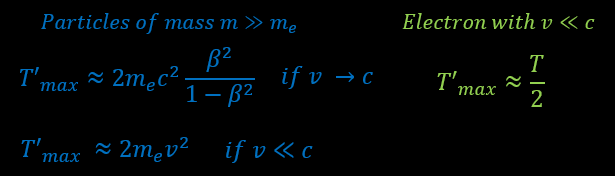
(for an incoming electron at relativistic speed v→c, remember that the Lorentz factor γ increase dramatically the mass of this electron, so T’max equation is the same that for heavy particle). And T’max =T/2 mean I don’t consider a head-on collision, otherwise T’max =T. The maximum energy is given to atomic electrons when the kinetic energy of the particle is high.
For a given medium, and assuming an incoming electron or proton or alpha particle is travelling in the medium, which of these particles have the most probability to make collisions to atomic electrons ? For a given kinetic energy T, let’s compare the value of β² and T’max between these particles :

Based on velocity β², the interaction probability φcol for a given energy T is much greater for a proton or alpha particle than for an electron. Based on the maximum energy which can be transferred, the interaction probability again is much greater for the heavy particles than for the electron. As an example, for particles of energy 1 MeV the collision probabilities would be in the approximate ratio :
Considering the above formulas, for given kinetic energy T of an incoming particle and atomic electrons in a given medium :
- Collision probability is low if the kinetic energy received by the atomic electron T’ is high. This is linked to low impact parameters that are scarce phenomenons. Thus, the number of high energy δ rays produced is very low compared to low energies δ rays, and much even lower versus the number of excitation or ionization (ejected electron that have almost no T’) produced by the incoming particle. It’s easy to observe this fact in a cloud chamber : count the number of delta ray in a single picture. For example in the proton’s track in the picture in top of this page, there is about 17 delta rays. But if I count the number of droplets which are in this tracks, I will get several thousands. Knowing that each droplets come from an ion produced by the excitation or ionization of the atom during a collision, the probability of this type of events are thousands time much more important than the probability to make a delta ray. So delta rays, are in a certain manner a rare process to observe.

Could it be an alpha particle, escaping from a Thorium welding rod, that kicked out an electron from an atom and gave him a great energy at the beginning of it’s track ?. Video (click here) No it’s impossible ! see the comments on youtube.
- Heavy particles are more likely to interact than are electrons. This explain why the ions density in an electron’s track is lower than a proton or alpha track. To precise, heavy particles « are more likely » to produce excitation and ionization of atoms ; more ions are created so more condensation occurs on them which produce thick tracks. So the brightness of an electron track is less than heavy particles.
- The energy transferred per collision is much less for heavy particles. Consequently, δ-ray production is much less. This explain why we rarely see in a cloud chamber a δ rays from an alpha particle. An α have about T=5 MeV and T’max would be 2,7 keV, the range for this ejected electron would be 0,2 mm → impossible to see this track. For an incoming proton of 20 MeV, T’max would be 44 keV, the range for this ejected electron would be 3 cm → we can see this track in the cloud chamber. As alpha particles are roughly 4 times heavier than proton and charged twice, they have a 4×2²=16 times more probability to make collisions, but the energy transferred to atomic electron are low, most of the energy transferred are by excitation and ionization.
- δ rays are likely produced when the speed of incoming particle is very low (see the 1/β² factor in equations) . Particles lose more and more energy as they travel in matter (see the dE/dx later in this page), so as β become very low towards the end of particle’s range, the probability of making delta ray increase with 1/β². Time of interaction with atomic electrons increase with decreasing velocity so the probability to make energy transfer is high. A delta ray can have an energy as low as 100 eV and it will be impossible to see this electron track outside the track of the main particle. The track’s width of a particle is caused by the range of these released electrons.
And finally, the maximum energy transferable to an atomic electron become lower with the decreasing energy of the particle.
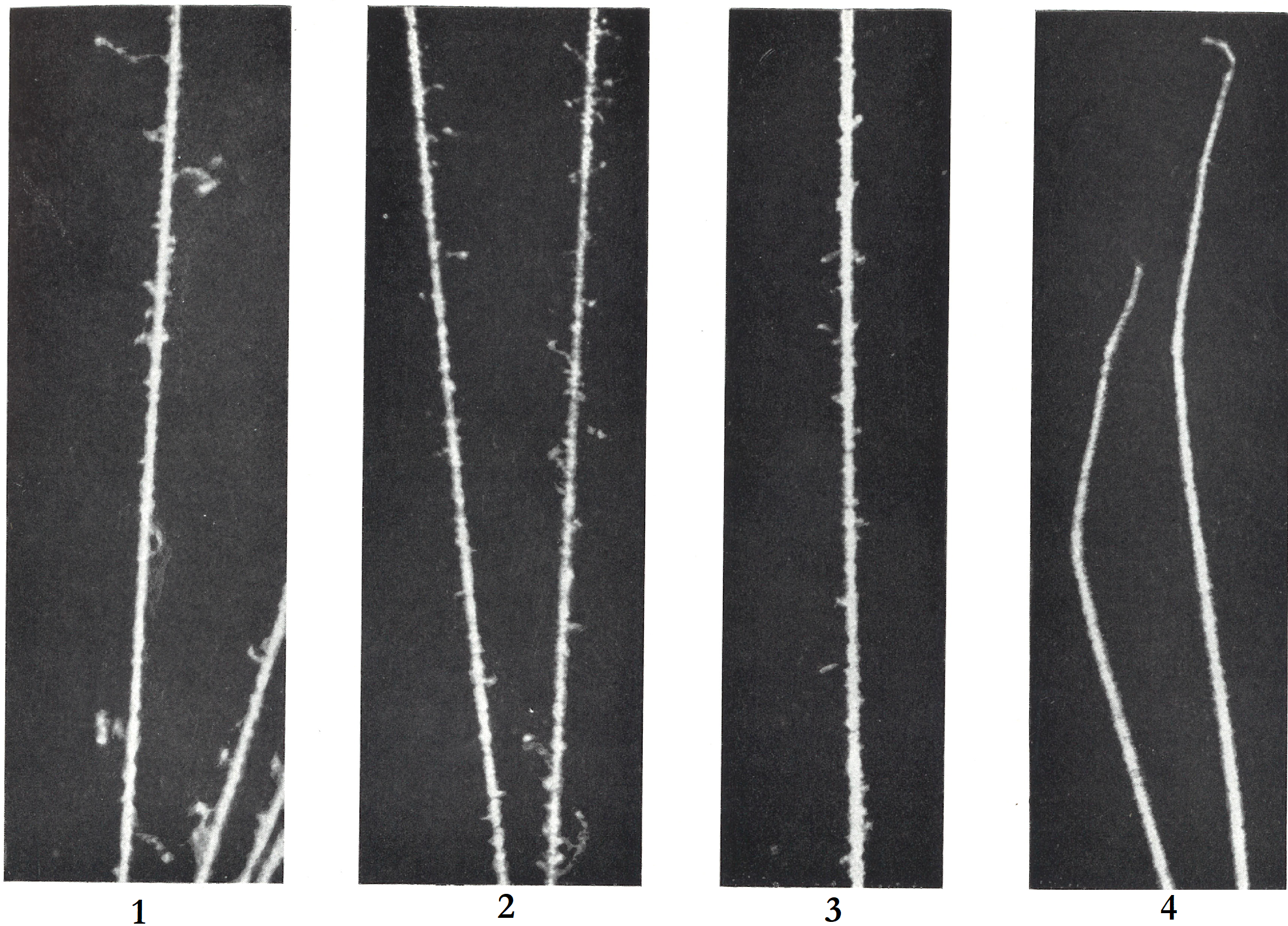
Left pictures (1932, expansion cloud chamber with a microscope) : the chamber was filled with air at a low pressure (1 cm Hg or 0,013 atm), except the picture n°1 where the pressure was higher. The low pressure allow to see δ-rays, a lower pressure increasing the visual range due to the reduced multiple scattering. The real height of the picture are 1 : 4,3 mm ; 2,3 et 4 : 1,5 mm. The energy of the alpha particle displayed in picture are 1 : 7,7 MeV ; 2 : 5,3 MeV ; 3 : 2,6 MeV. The picture 4 is the end of range of the alpha particle. No δ-rays can be seen near the end of range (as stated above, maximum energy transfer is low when the kinetic energy of particle is low). Comparison of the pictures 2,3 and 4 show clearly that the maximum range of δ-rays decreases with decreasing energy of alpha particle.
When a particle of charge ze, velocity v, passes through a material medium, the number of electron of energy >T’ which it projects a δrays, per unit length of trajectory, is given approximately by the relation :
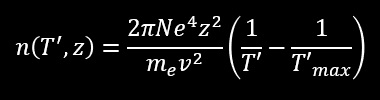
This formula resume that the number of delta ray increase if the particle have a low velocity v, have a high charge z and give a small energy T’ to the delta ray. Delta ray can have an energy as low as 100 eV. Considering a cloud chamber, an electron of 100 eV would travel less than a hundred of μm in air, so it won’t escape the thickness of the track. But as many delta ray are produced, the thickness of the track get bigger. So, by measuring the thickness of a track, or counting the grains of AgBr in an emulsion, we can discriminate two particles which have nearly the same mass but different charges as the number of delta ray increase with z². Example here. If you go back to the first picture of this page, you will understand why the tracks of the proton is thinner than the alpha track : the alpha produce more low energy delta ray than the proton due to it’s charge, so the alpha track appears bigger. Another example with a Calcium nucleus colliding in a photographic emulsion.
Angle of emission of delta ray
It can be shown that electrons of energy T’ are ejected at an angle θ to the trajectory of the incoming particle by the expression :

A proton travelling in across the cloud chamber created 2 δ rays. But what’s its direction of motion ?
If we consider a delta ray of energy T’max , cos² θ = 1 so θ=0° so from the trajectory of the incident particle,
- The least energetic delta rays will be produced at angles close to 90°,
- The most energetic delta ray will be produced at few angles from the trajectory.
From the equation about φcol(T, T’), most of the ejected electrons have energies much less than T’max . According to the equation with cos²θ, they should have ejection angles approximately equal to 90° to the track direction. So as δ rays can’t be produced at angle > 90° to the track direction, we can know the direction of motion of the incoming particle just by looking at the angle of δ rays. In the previous picture, two δ rays are produced at θ’≈60° and θ≈ 45°. Drawing a normal to the proton’s track and looking at the θ angles, they can only be < 90° if the particle is coming from left to right. And by measuring the angle and knowing T’max it’s possible to calculate the energy T’ of the delta rays.
The energy loss per unit path length dE/dx
It would be useful to have a formula which tell what is the average energy loss (MeV per cm) of a particle going in matter. Thus by measuring the length of path of a particle in the cloud chamber, we can determinate its initial kinetic energy. Note : E is the initial kinetic energy, so E=T in what follow.
φcol(T, T’) describe the collisions probability of charged particles via hard collisions (ejection of atomic electrons). In the total picture of charged particle collisions, hard collisions are comparatively rare versus the process of soft collision (excitation of atoms) and do not have much influence upon the most probable energy loss. However, this should not be interpreted to mean that they are unimportant since each hard collision carries away a relatively large amount of energy when it does occur. The average energy loss per unit path length (also known as the stopping power) from ionization and excitation is given by :
This formula comes from the integration of φcol(hard) and φcol(soft) over the values of T’ + corrections of various atomic effects. The sign « – » mean an energy loss for the particle. Term I is the mean excitation energy of material. For air it’s about 86 eV. This quantity describes how easily a target, typically a molecule or atom can absorb kinetic energy from the projectile, primarily as electronic (including ionization) and vibrational excitation.
Cette équation a été proposée par Bethe en 1932. La formule est valable pour une particule incidente de 0,1<βγ=p/mc<1000. A plus haute énergie, il faut prendre en compte les pertes radiative (Bremsstrahlung, important pour les électrons) voir nucléaire (collisions élastiques avec les noyaux du milieu qui recule sous l’impact de la particule incidente, cette contribution est importante pour les particules lourdes à basse énergie).
Pour un matériau donné on peut écrire que la perte d’énergie d’une particule dépend essentiellement de sa charge et de sa vitesse (a est une constante) :
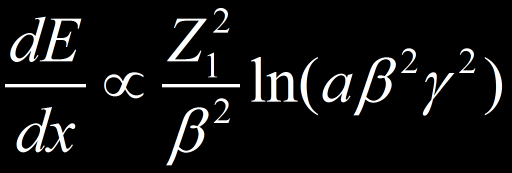
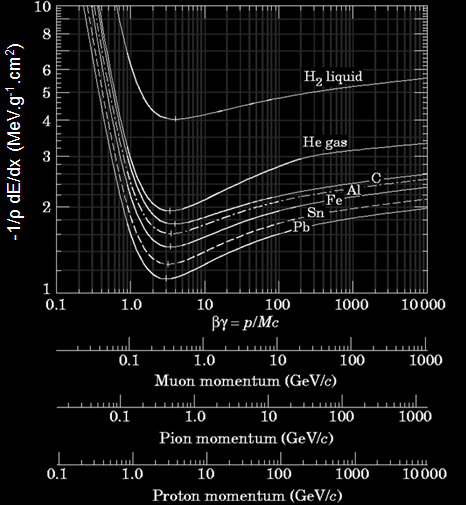
La courbe ci dessous à été calculée à partir de l’équation de Bethe dans l’air pour des particules de masses différentes. Lorsque la vitesse de la particule est faible (< 10 MeV pour des muons sur la courbe), on constate que la perte d’énergie de la particule est linéaire et est proportionnel à Z²/v² , Z étant la charge de la particule et v sa vitesse. Cette proportionnalité n’est valable que jusqu’à une énergie limite qui correspond au minimum d’ionisation de la particule (environ 2 keV/cm dans l’air). Pour un proton, la dépendance en Z²/v² de la perte d’énergie est valable jusqu’à 100 MeV, pour les alpha, jusqu’à 1000 MeV.
Cette proportionnalité en Z²/v² couvre une large gamme d’énergie ce qui permet de discriminer des particules à partir de la mesure de leurs pertes d’énergie dans la matière. Dans la chambre à brouillard, la perte d’énergie se matérialise par la formation des ions ce qui se traduit par une densité en gouttelettes plus ou moins importante suivant le nombre d’ions créés : la trace d’une particule perdant beaucoup d’énergie sera plus dense en gouttelettes que celle d’une particule perdant moins d’énergie.
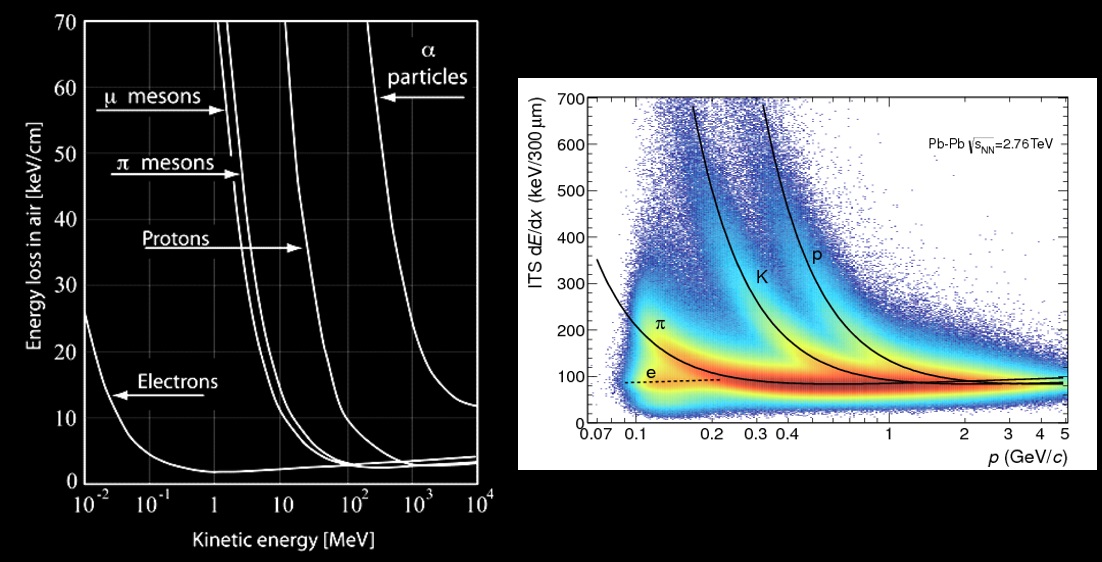
Left : La courbe de perte d’énergie par collision inélastique dans l’air de différentes particules, calculée à partir de l’équation de Bethe (les pertes radiatives ne sont pas prise en compte) Right : Distribution of the energy-loss signal in the ALICE CERN detector as a function of momentum. Both the energy loss and momentum were measured by the detector alone. Note : particles which have the same kinetic energy don’t imply that they have the same velocity ! Energy loss is proportional to z²/v² not to kinetic energy. Note that the energy loss of muon and pion is nearly the same : it’s because these particle have nearly same mass (106 vs 140 MeV/c²).
We can observe the same type of curves also in photographic emulsions. The image below show 6 tracks of pions at 6; 9; 17; 22; 29 and 33 MeV of velocity from left to right. If the particle have a low kinetic energy (for example 6 MeV for a π, β=0.28), the particle will lose a great amount of energy in the emulsion, producing a lot of silver grain (the black dots in the tracks). If the speed of the particle is rising, it lose less energy in the medium : the track is discontinuous and have few silver grain.
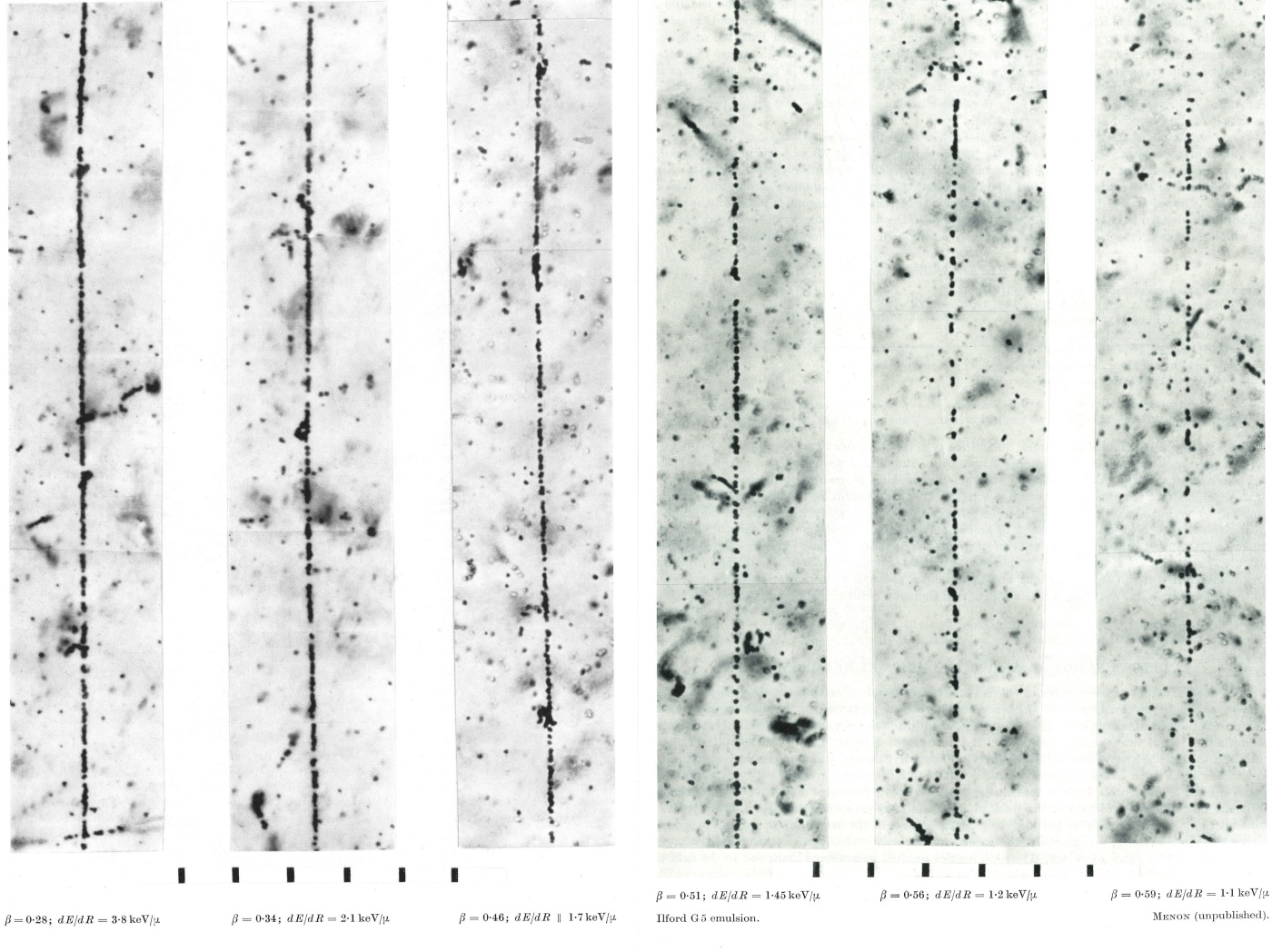
Grain density in the track of a pion for different value of its velocity. Ilford G5 emulsion. Compare the number of grains in the track between a slow particle (left) to a fast particle (right). Clic for more details.
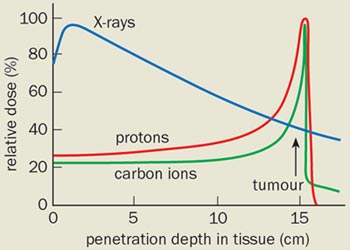
La proportionnalité en Z²/v² permet d’identifier la direction de déplacement de la particule. En effet, lorsque la particule se déplace dans la matière, elle perd peu à peu de son énergie à mesure qu’elle rencontre des électrons atomiques. Sa vélocité diminue, et le rapport dE/dx ≈ Z²/v² indique que le dE/dx augmente fortement à mesure que v diminue : dans un tracé, la présence d’une large densité (donc une grande ionisation) indique la fin de la trajectoire de la particule car sa vitesse y est très lente c’est le pic de Bragg.

Différence de densité sur le parcours d’une particule alpha. En haut de la trajectoire, le contraste est maximale indiquant que beaucoup de gouttelettes ont été crée.
L’image ci dessus illustre le phénomène. On observe une particule alpha et un électron. Si l’on s’intéresse à la particule alpha, on constate que la densité d’ionisation est plus forte en haut de l’image, le dE/dx y est donc plus important. La particule alpha s’est donc dirigée du bas de l’image vers le haut. L’accroissement soudain d’ionisation correspond au pic de Bragg.
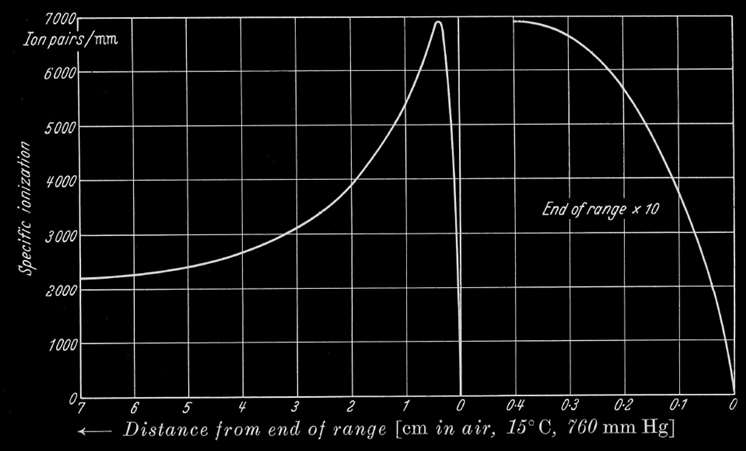
Quantité d’ionisation d’une particule alpha par rapport à son parcours. La particule est émise a l’origine de l’abscisse.
La courbe ci contre illustre la densité d’ionisation laissée par une particule alpha dans l’air en fonction de son parcours. Vers les derniers centimètres de son parcours, elle dépose énormément d’énergie en une faible distance, c’est le pic de Bragg.
Cet effet est utilisé en radiothérapie pour traiter les tumeurs, en les
bombardant avec des ions. En connaissant la distance de la tumeur dans les tissus, on s’arrange pour que les ions (protons) déposent le maximum d’énergie dans la tumeur via le pic de Bragg, sans trop irradier les tissus sains en amont de la cible (image de droite).
On peut préciser qu’il est très difficile d’observer un pic de Bragg sur le parcours d’un électron. Le pic n’apparaît que lorsque l’électron à une énergie inférieur à 1 keV ce qui correspond à un tracé d’une longueur d’une centaine de micromètre, difficile de détecter.
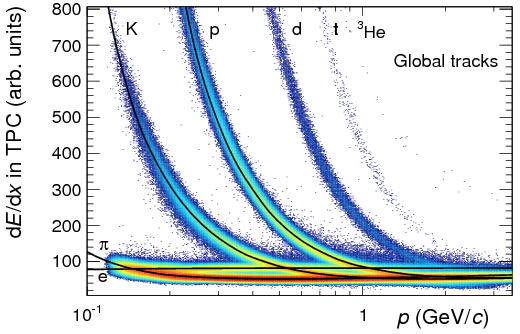
Perte d’énergie de diverses particules mesurée dans un gaz par la Time Projection Chamber du detecteur ALICE au LHC
En observant la courbe du dE/dx, on constate que même si deux particules ont une masse différente (par exemple un kaon et un proton), celles ci perdront la même quantité d’énergie dans la matière lorsqu’elles auront atteint chacune une vitesse déterminée : c’est le minimum d’ionisation. Un Kaon (masse 493 MeV/c²) ayant un momentum de 0,8 GeV/c (soit Ec=446 MeV avec v=0,85c) perdra la même quantité d’énergie (environ 100 dE/dX en unité arbitraire sur la courbe) qu’un proton (masse 938 MeV/c²) de 2 GeV/c (Ec= 1,2 GeV, avec v=0,9c).
La perte d’énergie linéique est proportionnel au carré de la charge de la particule. A vitesse égale, une particule alpha perd 4 fois plus d’énergie qu’un proton. Mesurer la densité d’ionisation d’une trace permet donc de remonter à sa charge comme illustré dans l’image ci dessous (on considère que les vitesses de ces noyaux cosmiques sont sensiblement égales en étant relativiste).
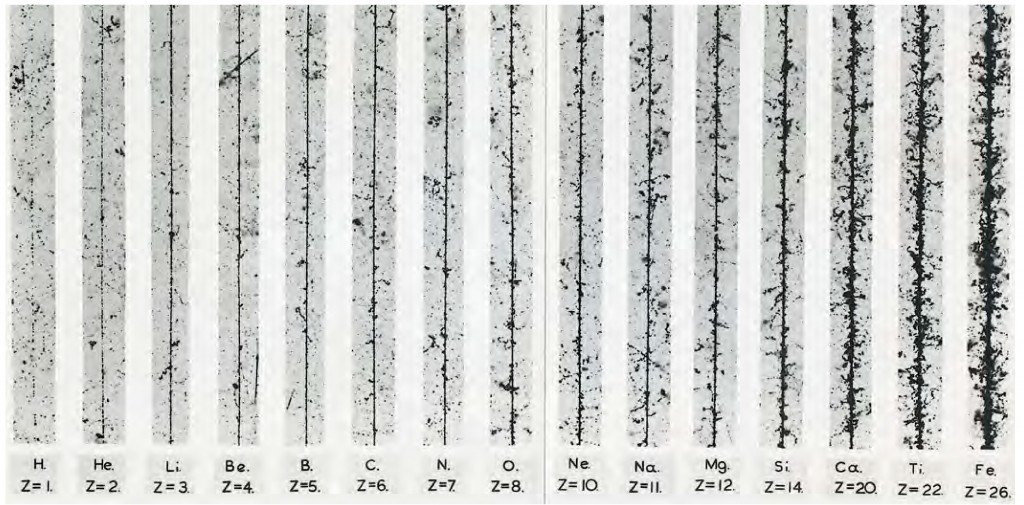
Noyaux cosmiques traversant des plaques à émulsion en très haute altitude. Ces noyaux sont chargés suivant leur Z. Lorsqu’un de ces noyaux traverse la plaque à émulsion, ils ionisent les cristaux de bromure d’argent ce qui libère de l’argent métallique là où l’énergie de la particule a été déposée. La trace de la particule est donc matérialisée dans ce milieu solide, et plus il y a d’ions d’argent formés, plus la particule a déposée d’énergie. Un noyau d’Hydrogène est chargé une fois ce qui laisse une trace peu visible. Un noyau d’Helium (alpha) chargé +2 créera 4 fois plus d’ions argent que l’Hydrogène. Un noyau de Fer crée une trace 676 fois plus dense (26²) qu’un proton. Ces noyaux proviennent de la galaxie et bombardent les hautes couches de l’atmosphère, environ 90% des noyaux sont de l’Hydrogéne, 9% des noyaux d’Helium, le reste est constitué des noyaux composant l’intégralité du tableau périodique.
Les pertes radiatives pour les muons et pions ne sont pas prises en compte
Si l’on s’intéresse aux variables de l’équation de Bethe, on constate que la perte d’énergie des particules lourdes dépend peu de la nature du matériau. En effet, le rapport Z/A (cf formule) est à peu près égal à 0,5 pour une grande quantité d’éléments (exemple Aluminium Z=13 et A= 27 g/mol soit Z/A = 0,48 pour ρ=2,7 g/cm3 ; Plomb Z=82 et A = 207 g/mol soit Z/A = 0,4 pour ρ=11,3 g/cm3 ).
En traçant la courbe (ci-contre) 1/ρ dE/dx en fonction du βγ=p/Mc de la particule (p est le momentum, M la masse de la particule au repos) , on constate que la perte d’énergie dépend peu du matériau où circule la particule. On peut retenir que la perte d’énergie minimum est en approximation égale à 2 MeV.cm²/g pour une particule de charge Z1=1, et ce quelque soit la nature (solide, gaz, liquide) du matériau traversé.
Pour obtenir la perte d’énergie linéique de la particule en MeV/cm il faut prendre en compte la densité d’électrons rencontrés par la particule et donc multiplier par la densité du matériau la valeur obtenue des pertes en MeV.cm²/g .
.
.
.
Exemple d’application :
Considérons un faisceau de pion d’énergie cinétique de 80 MeV traversant du carbone. Calculer l’épaisseur de carbone nécessaire pour stopper toutes les particules. Densité du carbone : 2,26. M(pion)=140 MeV. On définit E l’énergie totale de la particule, Ec l’énergie cinétique, p le momentum. On a E²=p²c²+M²c4 avec E0= Mc²
E=Ec+M soit E = 80 + 140 = 220 MeV.
βγ=p/Mc avec p²c²=E²-E0² soit p²c²=220²-140² soit pc= 170 MeV
βγ=170/140=1,21 . Sur la courbe précédente, on reporte la valeur du dE/dx correspondant à un βγ de 1,21 dans du carbone (si la courbe Carbone n’est pas présente, on aurait pris celle de l’Aluminium car on vient de voir que la perte d’énergie en MeV.cm²/g ne dépend que peu du matériau). On obtient dE/dx (βγ=1,21) = 2 MeV.cm²/g (environ).
Remarque : p=170 MeV/c = 0,17 GeV/c. La valeur du dE/dx s’obtient aussi avec l’abscisse en momentum du pion.
dE/dx (MeV/cm) = ρ (carbone) * 2 MeV.cm²/g = 2,26 g/cm3 * 2 = 4,5 MeV/cm
Chaque cm parcouru dans le carbone par la particule lui fait perdre 4,5 MeV d’énergie par collision inélastique avec les électrons du matériau. 18 cm de carbone suffit donc à stopper un faisceau de pion de 80 MeV d’énergie cinétique.
Les parcours des particules dans différents matériaux sont donnés sur cette page.
Perte d’énergie des particules lourdes par Bremsstrahlung
La physique du rayonnement de freinage est décrit ici.
La formule de Bethe n’est valide que pour une certaine gamme d’énergie (qui est très étendue et couvre toutes les énergies des particules rencontrées dans les chambres à brouillard). Cependant, pour β<0,05 (soit 1 MeV pour des protons) la formule n’est plus exacte et d’autres théories de perte d’énergie entrent en jeu comme le montre la courbe-ci dessous.
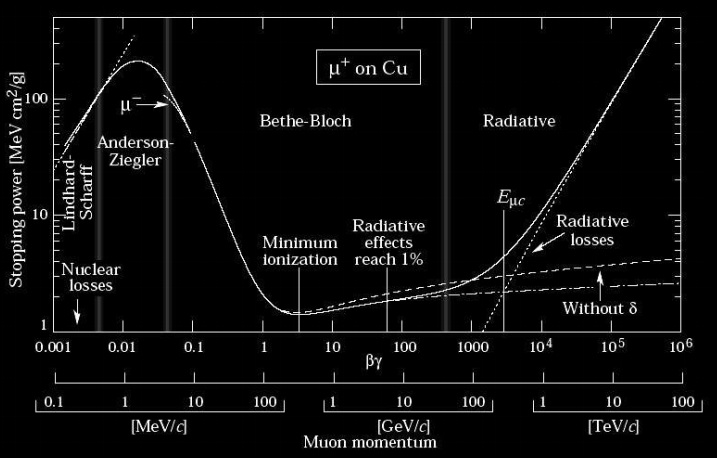
Perte d’énergie des muons dans du cuivre. Tous les processus de perte sont indiqués. Les pertes radiatives correspondent aux pertes par émission de rayonnement de freinage (les autres pertes comme l’émission Cerenkov ou les radiations de transition ne sont pas prises en compte, les pertes étant faibles). Pour obtenir la perte d’énergie linéique (MeV/cm) pour n’importe quel matériau il suffit de multiplier la courbe par la densité du matériau.
Sur la courbe, pour un βγ un peu inférieur à 100 GeV/c, la mention « radiative effects reach 1% » est présente. Cela signifie qu’à partir de cette énergie, les pertes radiative par Bremsstrahlung commencent à devenir non négligeables et atteignent 1% des pertes totales. Lorsque βγ=5000, Eμc est atteint (énergie critique muonique). Cela signifie qu’à cette énergie, les pertes par Bremsstrahlung sont égales aux pertes par collision inélastique calculées par l’équation de Bethe. Passé ce seuil, les pertes radiatives seront supérieures aux pertes collisionnelles.
Le Bremsstrahlung ou « rayonnement de freinage » est un rayonnement émis lorsqu’une particule est déviée de sa trajectoire par le champ électrostatique d’un noyau. En accélérant elle rayonne de l’énergie sous forme électromagnétique. La perte d’énergie par Bremsstrahlung pour une particule chargée s’exprime comme suit :
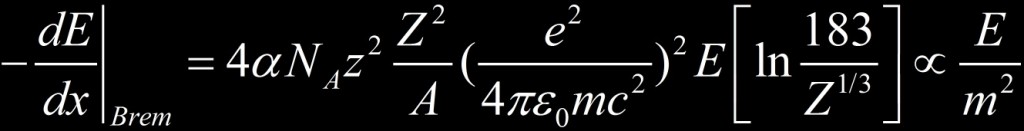
Les pertes radiatives sont plus importantes dans les matériaux denses (Z²) et avec des particules chargées plusieurs fois (z²)
L’effet n’est prédominant que pour de hautes énergies et est inversement proportionnel à la masse au carré de la particule. Si l’on compare la perte d’énergie par rayonnement de freinage à une énergie donnée pour un électron et un muon, le rapport de masse fait que le muon perd 43000 fois moins d’énergie par Bremsstrahlung.
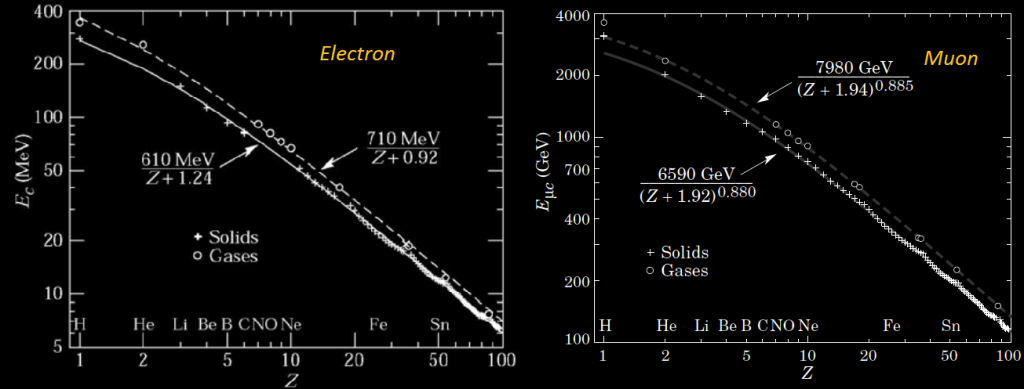
Les énergies critiques des electrons et muons se calculent suivant deux équations (milieu solide ou gazeux) :
Dans l’air Ec = 102 MeV pour un électron (7,5 MeV dans le plomb) et Ec=960 GeV pour un muon. Pour décrire la totalité des pertes d’énergie par un électron, il faut prendre en compte les pertes par Bremsstrahlung, et ce dès les basses énergies.
Nota : dans les emulsions nucléaires contenant en quantité égale des ions Ag-Br, Z ≈41 et Ec≈14 MeV.
Perte d’énergie des électrons par Bremsstrahlung
Le graphique ci-dessous illustre toutes les pertes possibles des électrons dans la matière. On reconnait la courbe de Bethe (« ionization ») et les pertes radiatives par Bremsstrahlung. Les autres processus d’interaction qui ne représentent qu’une faible perte d’énergie ne seront pas explicités (Moller, Bhabha).
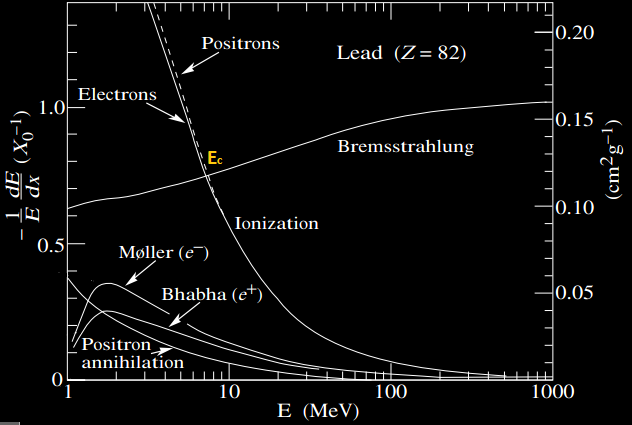
Perte d’énergie des électrons dans du plomb par unité de radiation X0. L’énergie critique est de 7,43 MeV.
Les pertes radiatives augmentent rapidement car elles sont directement proportionnelles à l’énergie de la particule. La longueur de radiation X0 en g/cm² est une constante calculée pour chaque matériau qui ne dépend pas de l’énergie de la particule. Au bout d’une longueur X0 (g/cm² /ρ = cm) parcourue par un faisceau de particule (électrons ou photons) :
- les électrons ont perdu 1/e (37%) de leurs énergies initiales par Bremsstrahlung,
- 63% des photons se sont convertis en paires e+,e- (après 9/7 X0).
Les longueurs de radiation pour tous les matériaux sont tabulés ici (dans l’air, X0=304 m). Ces valeurs sont valables pour les électrons/positons ainsi que les rayonnements gamma. Pour les autres particules (proton, pion, kaon, alpha, [sauf muons]…), on défini une autre valeur, la longueur nucléaire d’interaction (Nuclear interaction length) calculée à partir de section efficace d’interaction. Au bout d’une longueur nucléaire, le nombre de particules chargées a diminué d’un facteur 1/e. Les particules « manquantes » ont subit une interaction nucléaire inélastique (créant par exemple une cascade hadronique). La longueur moyenne d’interaction nucléaire dans l’air est de 750 m.
Les muons n’ont pas de longueur d’interaction nucléaire car ils n’interagissent pas avec la matière par le biais de l’interaction forte : ils ne peuvent faire de réaction nucléaire (spallation, cascade hadronique). Les pertes d’énergies des muons sont uniquement collisionnel (équation de Bethe) et radiatif à haute énergie. Il sont soumis à l’interaction faible et se désintègre en électrons ou positons suivant leur demie-vie.
Autre processus de perte d’énergie des particules lourdes
Les hadrons (proton, pion, kaon, hypéron) ou les ions (particule alpha…) du fait de leur très grande masse, ne sont peu ou pas soumis aux pertes par Bremsstrahlung. Par contre, ils peuvent collisionner (via un vrai choc) sur un atome et faire une réaction nucléaire. Les probabilités d’interaction sont régies par les sections efficaces d’interaction nucléaire prenant en compte :
- les collisions élastiques (avec conservation de l’énergie cinétique totale, exemple : diffusion d’un proton sur un proton, ou d’un alpha sur un noyau)
- les collisions quasi-élastiques (excitation d’un noyau par le projectile résultant en une perte minime d’énergie cinétique)
- les collisions inélastiques (non conservation de l’énergie cinétique, une partie de l’énergie de la particule est convertie en énergie interne dans la cible ce qui résulte en une spallation ou en la création de nouvelles particules).
Pour les deux premiers types de collisions, on défini la longueur de collision nucléaire λc, distance moyenne à partir de laquelle la particule réalise une collision élastique ou quasi-élastique. Dans l’air, la distance est de 508 m. Cette valeur est quasi indépendante de la nature de la particule.
Pour les collisions inélastiques, on définit la longueur d’interaction nucléaire λn qui se calcule par la formule ci-contre, avec A le numéro atomique du matériau. La longueur d’interaction en cm s’obtient en divisant le résultat par la masse volumique du matériau.
Dans l’air, cette distance est de 750 m, dans les solides, inférieur à 100 cm. On remarque que λn>λc car λn ne prend pas en compte les collisions élastiques et inélastiques. La portée d’un proton calculée à partir de l’équation de Bethe prenant en compte uniquement les pertes d’énergie par collision inélastique avec les électrons atomique est une portée théorique. En réalité, le proton aura probalement réalisé une interaction inélastique et aura perdu une grande ou la totalité de son énergie avant d’avoir parcouru la portée projeté par Bethe.
Exemple : un proton de 500 MeV à une portée maximum de 1095 m dans l’air avant qu’il ne perde toute son énergie par ionisation. Il faut rajouter les pertes par interaction nucléaire avec λn=750 m, ce qui signifie qu’en traversant 750 m d’air, le proton a une probabilité de 1/e= 37% de ne pas avoir d’interaction avec un noyau. Donc, un proton de 500 MeV à 37% de chance de parcourir les 1095 m.
Les hadrons « malchanceux » percutant un noyau au cours de leur parcours créeront des spallations ou des cascades hadroniques.
Conclusion
Nous avons vu que les électrons perdent leurs énergie par collision inélastique avec les électrons du milieu (Bethe) mais aussi par émission de rayonnement de freinage. Les muons étant 207 fois plus lourd que les électrons, ils ont les mêmes processus de perte d’énergie que les électrons sauf que les pertes radiatives ne deviennent prépondérantes que pour de très hautes énergies. L’interaction des muons dans la chambre à brouillard fait l’objet d’un article séparé.
Les hadrons (proton, pion, kaon…) et les ions (particules alpha…) sont au moins 10 fois plus lourds que les muons. Ils ne subissent que très peu de pertes d’énergie par Bremsstrahlung. Comme toutes les particules chargées, la principale perte d’énergie se fait par ionisation/excitation des électrons du milieu décrit par l’équation de Bethe. A ces pertes, il faut rajouter la possibilité qu’ils fassent des interactions élastiques ou inélastiques avec les noyaux qu’ils rencontrent. Dans ce dernier cas, seules les particules soumises à l’interaction forte (particules constituées de quarks) peuvent faire de telles réactions, ce qui n’est pas le cas des muons qui sont des particules élémentaires soumis uniquement à l’interaction faible (il sont instables et se désintègrent).
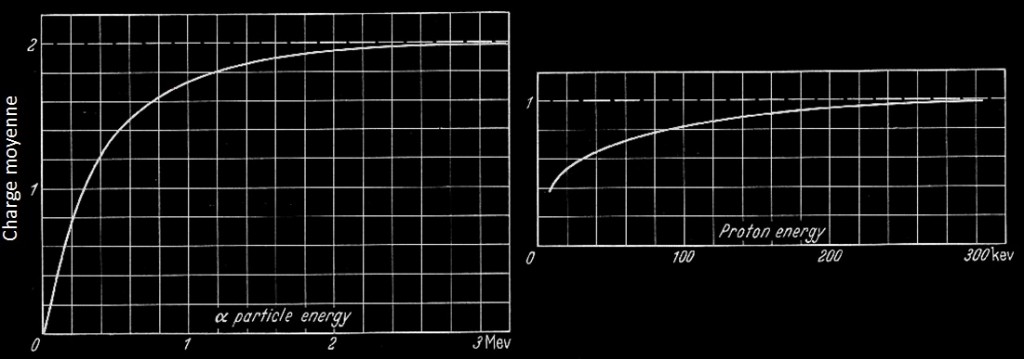
A propos de la charge des noyaux
Les protons et les particule alpha sont des noyaux et lorsqu’ils traversent la matière, ils ont tendance à capturer des électrons pour devenir des atomes d’hydrogène et d’hélium respectivement. Il en est de même pour les fragments nucléaire que l’on peut observer lors de spallation ou des noyaux du rayonnement cosmique (ions carbone, azote…) . Cette « capture électronique » ne se passe que lorsque les noyaux ont trés peu d’énergie cinétique. A mesure qu’un noyau se rapproche de l’électroneutralité, sa charge diminue et la perte d’énergie par ionisation proportionnel (pour des énergies pas trop faible) à z²/v² diminue et la traînée de condensation disparaît : le noyau est devenu un atome. L’effet peut se voir sur la photo ci dessous.

Fin de parcours d’une particule alpha dans une chambre à expansion sous 0,5 atm d’hydrogène, prise avec un objectif de microscope dans les années 30. The track of the particle has a certain width caused by the range of released electrons. Les pertes par ionisation diminuent à mesure que la particule alpha se rapproche de la neutralité (l’épaisseur de la trace diminue). The strong increase of nuclear scattering near the end of the range is very clear in this picture (nuclear scattering is proportional to the velocity of the particle).
Another example with 2 photographic emulsions showing the end of range of nuclei with high Z :
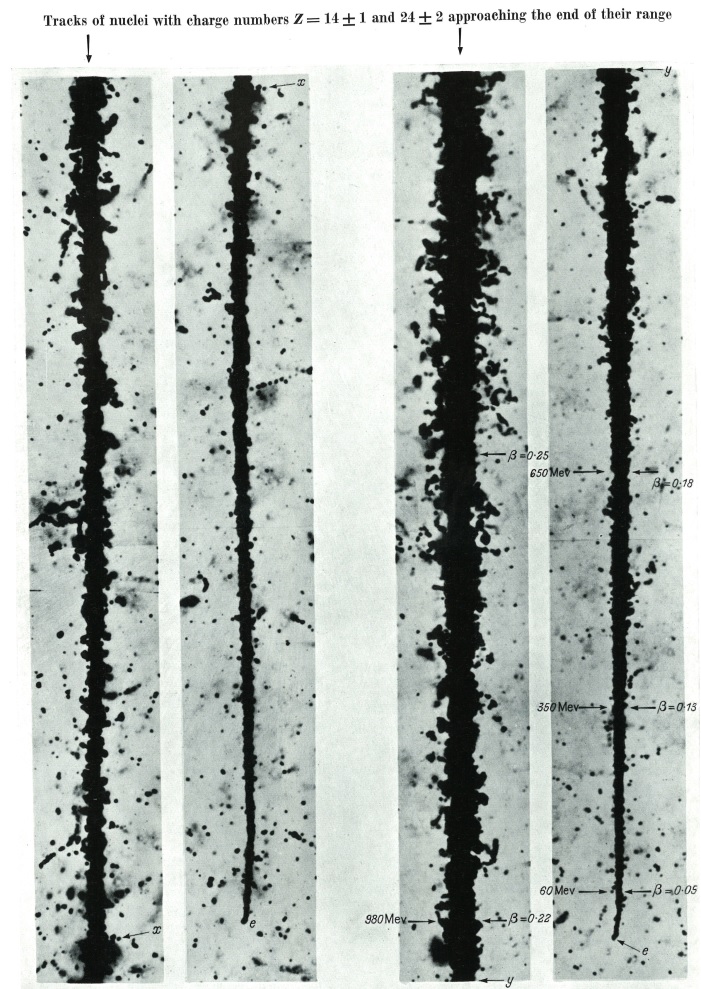
The track of carbon nucleus appears to terminate before it has become as thin as that of the nitrogen nucleus at the extreme end of the range. This is probably due to a nuclear collision in which the particle was scattered. The length of each photograph is 200 micrometer
For heavy nuclei, there is another phenomenon which appear before the end of the tracks. The track become bigger as the velocity decrease, but this increase of thickness is not related to the increase of the specific ionization . See this page for more pictures.