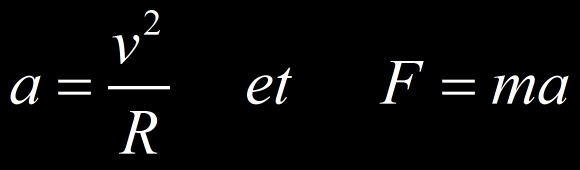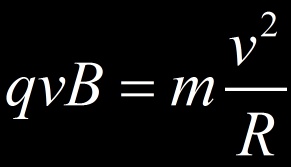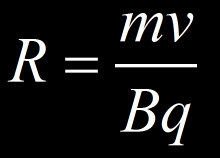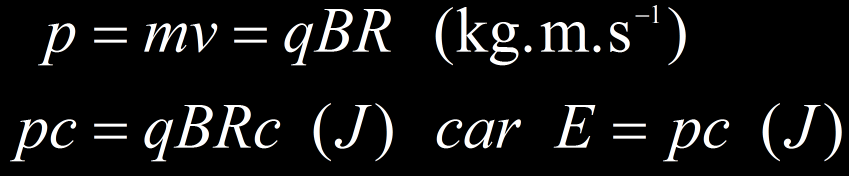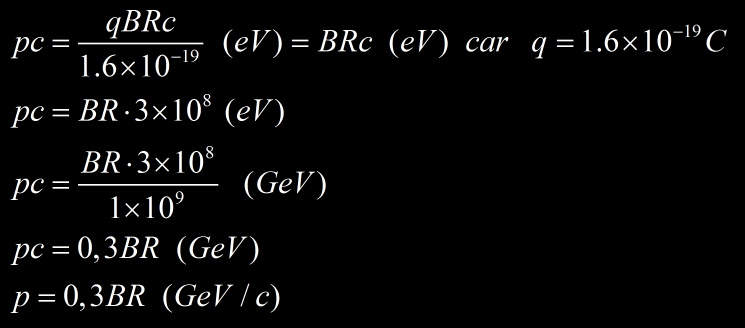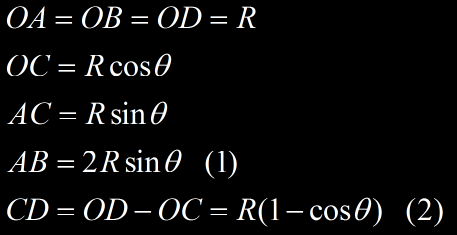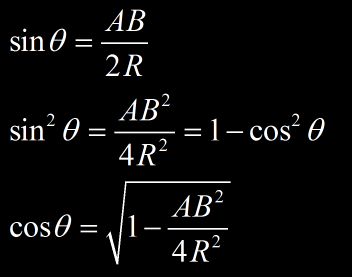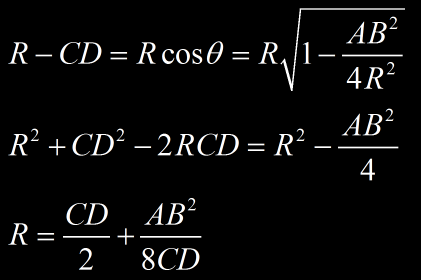A cloud chamber without magnetic field shows little interest. The Lorentz force will deflect the lightly charged particles, such as electron and positon, according to their charges (electron will deflect to left and positon to right, but this depend on the direction of magnetic field). The particles will describe « circles » where R is the radius of curvature. By mesuring R, you can rougly estimate the energy of the particle as you know it’s mass and the intensity of the magnetic field (R=mv/Bq and E=m02c4+p2c2).
The magnetic field is useful to detect the gamma annihilitation process (or pair creation). Without magnetic field, it’s impossible to say that we are looking at 2 differently charged particle (remenber that the pair creation process occurs only when the energy of the gamma is at last of 1.02 MeV, cosmic radiations will provide this energy). The next picture show what a pair creation look likes.
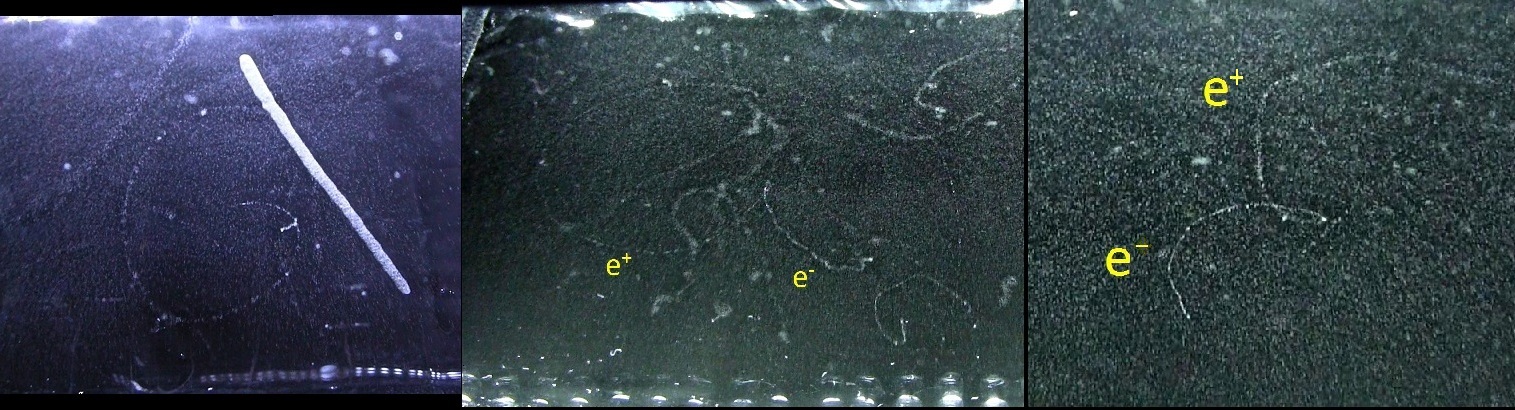
Left : an alpha particle is not subject to the magnetic field because this particle is too heavy to be deflected by the present field, but the electron is deflected (if they have energy < 1MeV which is often the case). Magnetic field can also discriminate muons from electron : Muons are 207 times heavier than electron so they are not subject to deflection (only if they have very low energy). Right : pair creation (gamma annihilation)
The magnetic field is provided in the chamber with a Neodymium magnet. Now the theory about the Lorentz force.
Lorentz Force
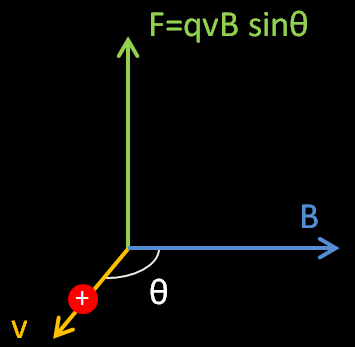
Si l’on considère un proton de charge q=+1,6×10-19 C se déplaçant dans un champ magnétique dont la direction est donnée par le vecteur vitesse B (les croix bleus indiquent que le pôle Nord s’éloigne de l’observateur), la particule subira une force perpendiculaire à la direction de son vecteur vitesse et du champ magnétique : c’est la force de Lorentz. Elle décrira une trajectoire sous la forme d’un cercle. La direction de la force centripète passe toujours au centre du cercle décrit par la particule, comme illustrée sur le schéma ci dessous.
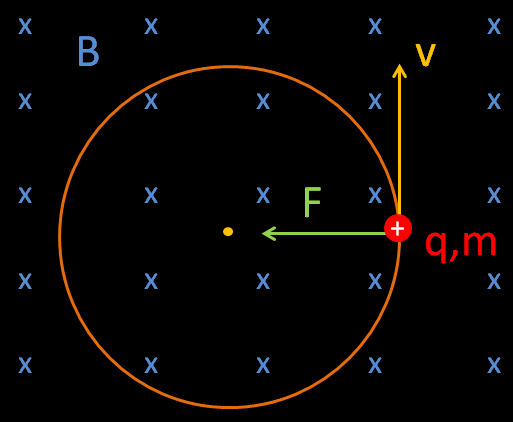
Trajectoire d’une charge positive (cercle orange) se déplaçant sous un champ magnétique
Il y a une accélération vectorielle (changement de direction), mais pas d’accélération scalaire (pas de changement de vitesse) lorsque la particule subit la force.
Note sur les observations : Pour qu’une particule chargée décrive une trajectoire circulaire dans un champ magnétique, il faut que sa vitesse soit perpendiculaire aux lignes de champ. Dans ce cas, la force de Lorentz agit comme une force centripète et la particule est déviée en permanence, formant un cercle dans un plan perpendiculaire au champ. Si la particule se déplace parallèlement aux lignes de champ (vitesse colinéaire à B) la force de Lorentz est nulle, et la particule poursuit sa trajectoire en ligne droite, comme si le champ n’existait pas. En pratique, dans une chambre à brouillard, le champ magnétique est créé par un aimant dont les lignes de champ ne sont pas uniformes : elles sont courbes, orientées du pôle nord vers le pôle sud et souvent inclinées par rapport au plan d’observation.
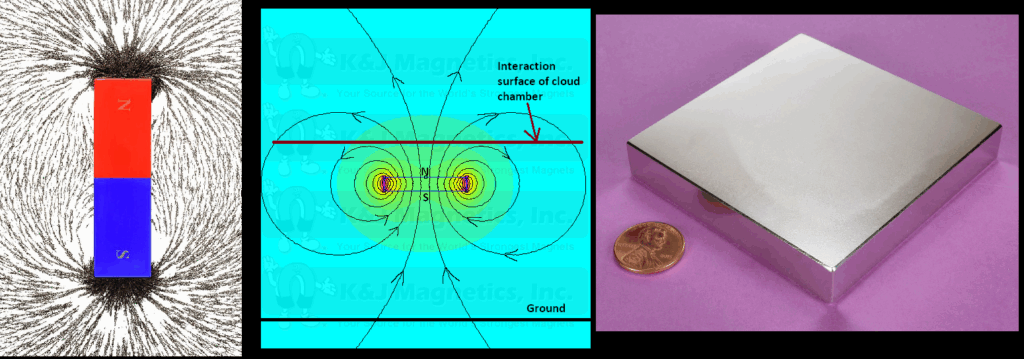
Le champ magnétique dans la chambre à brouillard est crée par cet exemple de magnet (parallélépipède) avec le Nord vers le ciel. On observe que les lignes de champ ne sont en fait jamais perpendiculaire par rapport au plan d’observation (où se trouve les particules).
Le vecteur champ magnétique B et la vitesse v de la particule ne sont donc généralement ni strictement colinéaires, ni parfaitement orthogonaux. Dans ce cas général, la trajectoire de la particule devient hélicoïdale : elle enroule une spirale autour des lignes de champ, à la manière d’un tire-bouchon. Ce type de trajectoire est particulièrement visible dans les régions où B est quasi vertical (par exemple, juste au-dessus de l’aimant) et où la particule se déplace principalement dans le plan horizontal. On y observe alors des courbures marquées dans le plan de la chambre.
Il faut aussi garder à l’esprit que la trajectoire réellement parcourue par la particule est tridimensionnelle, tandis que l’on n’en observe qu’une projection dans le plan où se forment les gouttelettes (le plan de sursaturation). Ainsi, l’inclinaison du vecteur vitesse par rapport à ce plan peut faire apparaître une trajectoire plus courte ou plus incurvée qu’elle ne l’est en réalité.
La force de Lorentz (analogue à une force centripète) s’exprime par :
Avec θ l’angle entre la direction du vecteur vitesse et du champ magnétique .
Pour que la particule soit soumise à la force la plus intense possible, il faut que sin θ = 1 ce qui est possible si θ=90°. Dans toutes les expériences mettant en oeuvre des déviations de particules, le champ magnétique est ainsi toujours perpendiculaire à la direction de la vitesse de la particule afin d’avoir la plus grande force possible. Il convient de préciser que la force de Lorentz agit perpendiculairement à la direction de la vélocité, c’est donc une force qui ne travaille pas : un champ magnétique ne fait que dévier la trajectoire une particule (elle tourne sans changer sa vitesse en norme seulement sa direction. Seul un champ électrique permet d’accélérer une charge.
La direction de la force dépend du sens du vecteur champ magnétique, du sens du vecteur vitesse de la particule et de la charge de celle ci. La direction de la force se détermine à l’aide de la règle de la main droite :
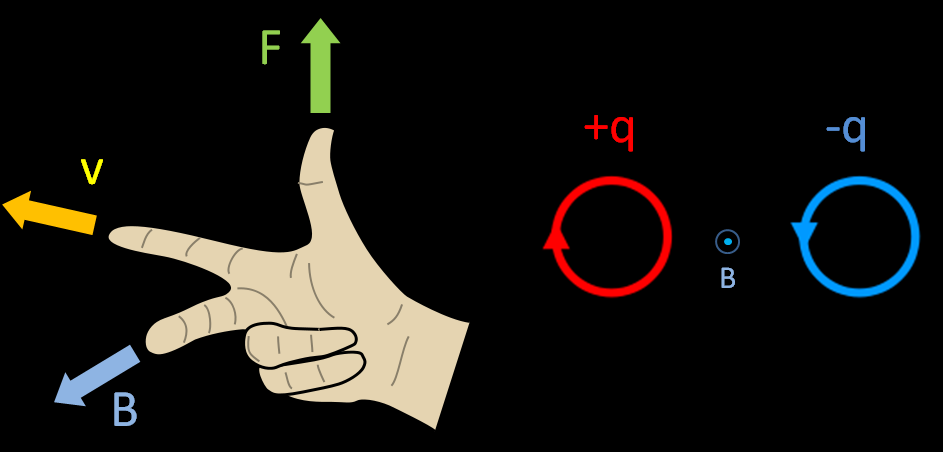
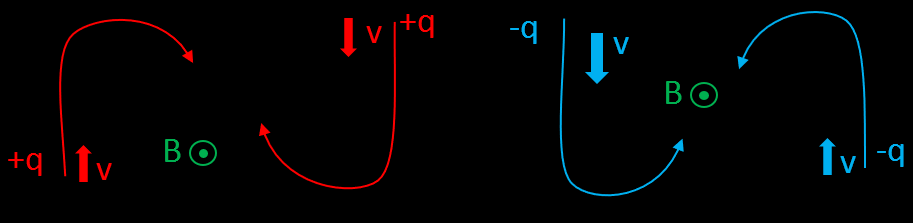
La « règle de la main droite » permet de déterminer la direction de la force de Lorentz. Le Majeure représente la direction du champ Magnétique, L’Index pour la vitesse, et le Pouce pour la force (car une force « pousse »).
Si l’on considère une charge positive (+q) se déplaçant vers le haut (ou le bas) de l’écran, avec la direction du champ magnétique venant vers l’observateur (on observe le pole Nord d’un aimant par ex.), la particule sera déviée « vers la droite » comme le montre le cercle rouge. A l’inverse, si la particule à une charge négative (-q) comme un électron, il faut inverser le résultat précédent : la particule est déviée « vers la gauche ».
Nous avons jusqu’ici considéré que les particules faisaient des cercles sous l’action d’un champ magnétique, sans modification de la vitesse de la particule. En réalité, le rayon de l’orbite (plus précisément le rayon du cercle osculateur) dépend de la charge, de la vélocité, de la masse de la particule et de l’intensité du champ magnétique.
Une particule soumise à une force F à effet centripète possède une accélération a qui s’exprime par :
Suivant la valeur des deux membres de l’équation, les particules décriront des rayons de courbure différent. On considère qu’une trajectoire droite à un rayon de courbure qui tend vers l’infini alors qu’un cercle à un rayon de courbure qui tend vers 0.
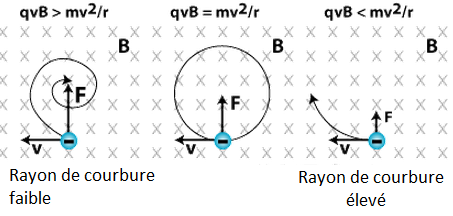
Avec m, B,q fixé, la variable de l’équation est la vitesse. Plus une particule est lente et plus sa trajectoire sera courbée (la trajectoire se rapproche d’un cercle). A l’inverse, plus une particule est rapide et plus le rayon de courbure est élevé : la trajectoire se rapproche de celle d’une droite.
On a le rayon du cercle osculateur (le cercle qui épouse au mieux la courbe à un point donné) qui s’exprime par :
Dans un monde idéal, on aurait donc une particule m, v, q qui ferait un rayon de courbure R en étant soumise à B. Cette valeur R serait constante. Or ce n’est pas le cas :
Une particule se dirige du haut vers le bas et à un moment donné commence à être dévié de plus en plus par le champ B
Comme on peut le voir sur l’image ci-dessus, le rayon de courbure de la particule diminue de plus en plus (la courbure se resserre de plus en plus). Il ne faut pas oublier qu’une particule qui à une trajectoire courbée doit conserver sa quantité de mouvement. Pour cela elle émet un rayonnement de type Bremsstrahlung tout au long de sa courbure. Elle perd donc progressivement de l’énergie sous forme de photons et donc de la vitesse. Cette perte énergétique entraîne une diminution de son rayon de courbure, conformément à la relation R=mv/Bq, puisque la quantité de mouvement (mv) diminue expliquant pourquoi la courbure est de plus en plus resserrée.
Il faut alors retenir que lorsque des particules sont déviées par un champ magnétique, elles perdent constamment de l’énergie par Bremsstrahlung en plus des pertes d’énergie par ionisation ! On peut prendre l’analogie avec un vaisseau spatial passant à coté d’un trou noir. En ligne droite, on consomme du carburant pour avancer normalement. Mais si on se rapproche du trou noir il nous attire ce qui nous fait décrire une trajectoire courbée et là on brûle encore plus de carburant pour vaincre la force centripète et reprendre une trajectoire droite. Un champ magnétique agis alors comme un piège, lorsqu’il attrape une particule il va la forcer a spiraler et en conséquence à brûler son reste d’énergie en rayonnement de freinage. Mais certaines peuvent s’en échapper !
A pair creation occured in the bottom left of the picture. With the direction of B, negative particle goes to the left but the electron don’t go far away and make just a little spiral. The positon is deflecting to the right. It received a lot of energy from the pair creation process as its track is longer than the electron. At the end of its path, the positron escaped from the influence of the magnetic field and make now a straight track (he escaped from the black hole 🙂
Note sur les observations : dans le vide, une particule sera systématiquement déviée dans une direction précise et prévisible par le champ magnétique. Cependant, pour les chambres à brouillard atmosphérique, le milieu d’évolution est de l’air où la particule peut faire de nombreuses diffusions multiples sur les noyaux ou électrons. Ces interactions perturbent la trajectoire en modifiant localement la direction de la vitesse ce qui peut parfois engendrer une courte trajectoire dans une direction opposée à celle attendue dans le champ magnétique.
The red-marked images show events where the delta rays or electrons deviate correctly to the left, following the direction of the magnetic field. However, sometimes delta rays do not follow this expected deviation, even when they appear in the strongest region of the cloud chamber where the magnetic field is present. These are the events highlighted in yellow. The arrow indicates that the delta ray should have been deflected to the left, but instead, it is deflected to the right. Multiple Coulomb scattering can sometimes cause incorrect identification of the particle’s charge, so we cannot always rely on the curvature direction to determine it.
Another example :
An incoming particle at A and moving to A’ (a positon, as its deviated to the right) encounter an atomic electron at B and make a delta ray. This delta ray is not deflected until the point D in the good sens of deviature, as it should be deviated to the left with the magnetic field.
A partir de la relation R=mv/Bq, on peut remonter à l’énergie de la particule en mesurant le rayon du cercle et en connaissant la masse, la charge de la particule et l’intensité du champ magnétique.
Déviation des électrons émis d’une source de Sr90 dans la chambre à brouillard thermoélectrique. Le vecteur champ magnétique est perpendiculaire au plan d’interaction et son sens est dirigé vers l’observateur. Les électrons se dirigent de bas en haut et sont donc déviés vers la gauche d’après la règle de la main droite.
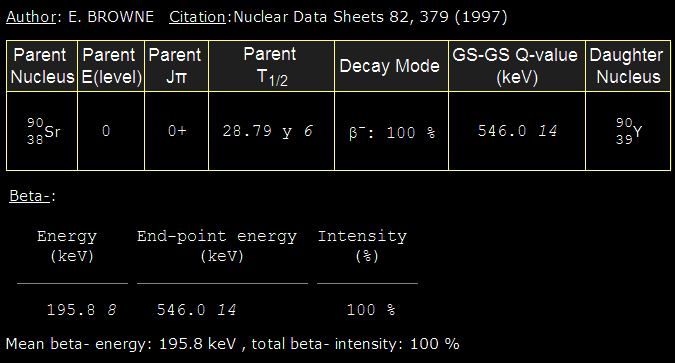
A m,B,q constant, le rayon de courbure dépend essentiellement de la vitesse de la particule. Plus la particule est rapide, moins elle subit l’influence du champ magnétique et moins elle « courbe ». On peut observer cette tendance dans la chambre à brouillard, en mettant une source d’électron « émis à énergie variable » (photo ci contre). La source est ici du Strontium 90, source « bêta pure » (la désintégration du Strontium en Yttrium ne génère que des électrons). L’énergie cinétique des électrons de désintégration varie entre 0 et 546 keV (portée max dans l’air : environ 1,6 m). Le reste de l’énergie est partagée avec un anti-neutrino. On observe sur la photo que certaines trajectoires électroniques sont plus déviées que d’autre par le champ magnétique, car les vitesses des électrons sont différentes. La flèche jaune indique une trajectoire avec un rayon de courbure faible, tandis que la flèche verte montre une trajectoire avec un rayon de courbure élevé : cette dernière trajectoire correspond au passage d’un électron rapide, tandis que la trajectoire indiqué par la flèche jaune correspond au passage d’un électron plus lent.
.
Il est parfois commode d’exprimer en fonction du momentum le rayon du cercle osculateur. Le développement suivant est valable pour une particule de charge |q|=1 (électron, proton, muon…), et dans des situations relativistes ou non relativistes.
Il suffit de connaitre B et R pour obtenir la quantité de mouvement p=mv de la particule. Le momentum est exprimé en GeV/c si B est en Tesla et R en mètre. L’intensité du champ magnétique est déterminée par les conditions expérimentale (il peut s’agir d’un aimant ou d’un électroaimant) et le rayon du cercle osculateur s’obtient par mesure sur la trajectoire d’une particule.
A titre d’exemple, une particule de momentum 1 GeV/c décrit un cercle de rayon R=1,11 m dans la chambre à bulle du Fermilab (diamètre de la chambre = 4,4 m). Le champ magnétique était de 3T (images ci dessous).
Les deux photos de gauche montrent l’assemblage de l’aimant supraconducteur refroidi à Helium liquide et produisant 3T en son centre. La chambre à bulle de 4,6 m était placée à l’intérieur de l’aimant. Elle fut construite en 1973 et démantelée en 1988 après avoir photographiée 3 millions d’événements.
.
Mesure du rayon du cercle osculateur ou du « rayon de courbure R »
Lorsqu’un électron traverse un champ magnétique, sa trajectoire est courbée. Mais l’intensité du champ magnétique varie rapidement suivant la géométrie de l’expérience et donc la courbure de la trajectoire de la particule varie également. L’équation précédente permet de calculer la quantité de mouvement d’une particule en mesurant son rayon de courbure en un point donné, en traçant le cercle osculateur en ce point. Le cercle osculateur est le cercle qui « épouse la courbe le mieux possible » au point donné. Sur la figure ci dessous, W désigne le cercle osculateur au point de la trajectoire D. Le rayon R du cercle est le rayon de courbure de la courbe en D. La quantité de mouvement calculée à partir de la courbure (AB) correspondra uniquement à cette portion de trajectoire de la particule. Pour calculer la quantité de mouvement à un autre point de la trajectoire de la particule, il faudra tracer un nouveau cercle osculateur et déterminer R.
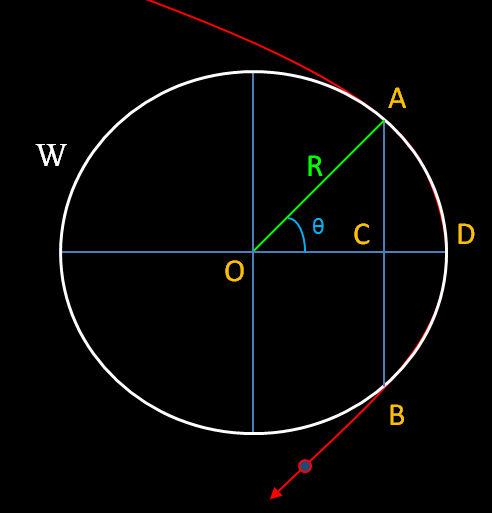
Cercle osculateur W épousant au mieux la courbure de la trajectoire (en rouge) d’une particule au point D.
Calcul du rayon de courbure R
On a :
Dans (1) :
Dans (2) :
Cas pratique : calcul de l’énergie cinétique de la particule dans la chambre à brouillard
On considère l’image ci dessous. Il s’agit de la trajectoire courbée d’un électron sous un champ magnétique, émis par une source de Sr 90. Cette expérience à été faite dans une version de chambre à brouillard plus ancienne que celle présentée sur le site. A l’époque, la surface d’interaction mesurait 12×8 cm. Peut t-on estimer l’énergie cinétique de la particule traversant la chambre ?
On peut observer deux trajectoires d’électrons. L’une est plus courbée que l’autre, ce qui indique que la particule à moins d’énergie cinétique. Le calcul portera sur l’électron dont la trajectoire est la plus courbée
Pour calculer le momentum de la particule, il faut obtenir le rayon de courbure. Ce dernier se calcule en mesurant les distances AB et CD. Pour effectuer des mesures précises de distance, il aurait fallut indiquer des marques sur la surface d’interaction comme le font les physiciens dans les chambres à bulles. Néanmoins, par construction, la longueur de référence de 4 cm est connu (elle correspond à la largeur d’un peltier). Sur la trajectoire on relève la distance AB, qui vaut ici 3,7 cm. La distance CD mesure 0,8 cm. On calcule (suivant la formule précédente) que le rayon de courbure vaut R=2,5 cm.
L’intensité du champ magnétique peut être estimée à 100 mT d’après l’aimant utilisé. Le calcul du momentum donne :
- p=0,3BR=0,3 x 0,1 x 0,025 = 0,75 MeV/c
En utilisant l’équation définit dans la page de la boite à outils relativiste, on peut calculer l’énergie cinétique de la particule, sachant qu’il s’agit d’un électron.
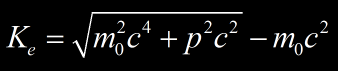Soit Ke=(0,511²+0,75²)1/2 – 0,511 = 0,396 MeV
L’électron à une énergie d’environ 400 keV (aux incertitudes près !).
Le Strontium 90 émet des électrons à une énergie maximale de 546 keV. L’autre électron dont la trajectoire est moins courbée sur la photo précédente, est plus énergétique et à donc une énergie comprise entre 400 et 546 keV.
.
.
.
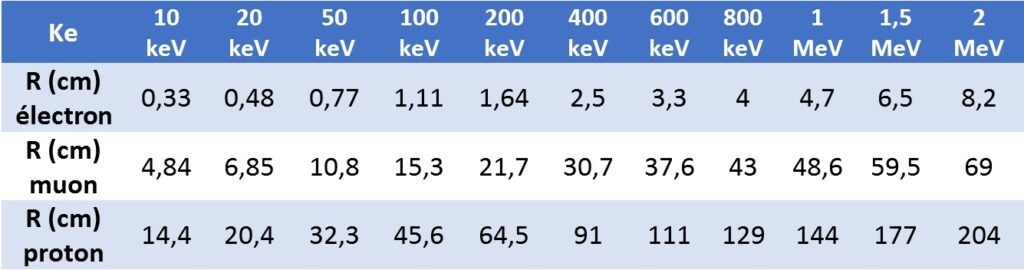
Radius of curvature for 3 particles and a B field of 100 mT :
What an electron with a magnetic field of 0,1 mT could make as deviation in a 400×200 mm cloud chamber :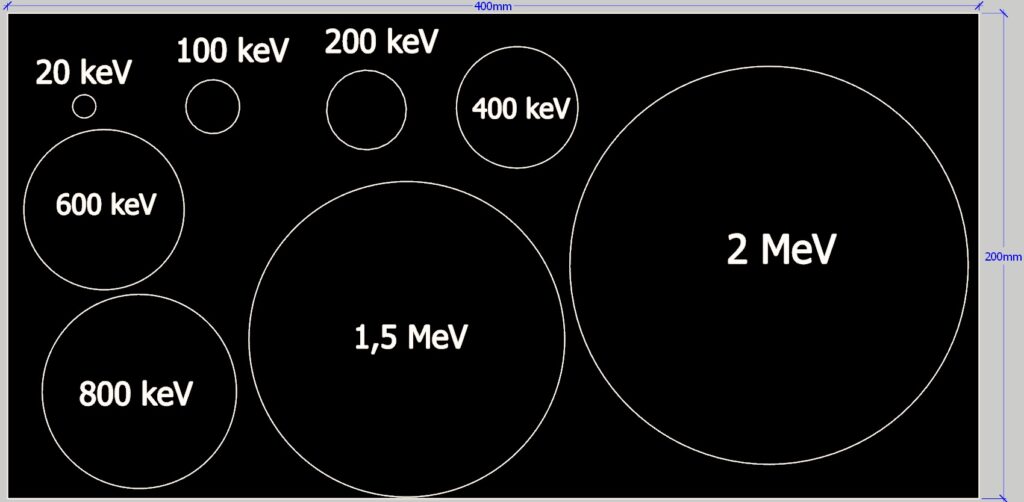
Using Google Sketchup to know the energy of an electron
Imagine for example that you have a cloud chamber which have an interaction surface about 400 x 200 mm. The frame below come from a movie recording cosmic rays with a magnetic field of 0,1 Tesla and you want to know what is the energy of the deviated electron D. At A, we have a particle which go straight in the chamber and is largely deflected at point B, by creating a delta ray. In this process the particle A can lose up to the totality of its initial energy. The delta ray (atomic electron) then make its own track C. The particle A continue its path after point B, after losing a substantial amount of energy. This low energy implies that the particle is now sensible to the magnetic field (it was not before at A) and make a deviation. What could be the energy of this particle, a positon with the sens of curvature, at D ?
We can use Google Sketchup to measure the radius of curvature.
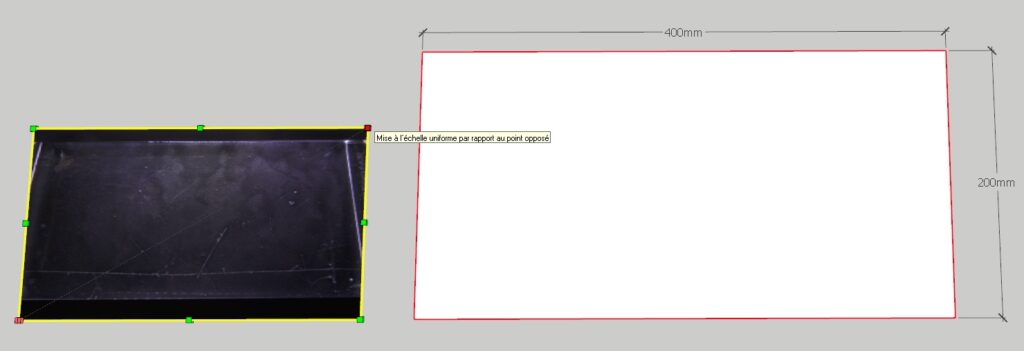
Step A : import the picture in Sketchup, then make a rectangular form of the size of the interaction surface of your chamber. Here, it’s 400×200 mm. Give this rectangular a thickness of about few mm.
Import and make a rectangular plan of 3 mm thickness
Step B : Displace the plan 1 mm above the picture, and make them approach each other.
The plan is 1 mm above the picture
Step C : Use the scaling tool of sketchup to upsize the image until it fit the dimension of the plan.
Upscale the picture and displace it until the interaction surface meet the dimension of the plan
There it fit. We have the perspective of the camera, so the error are great but this will give the order of magnitude and the idea.
Step D : Place the plan under the picture.
Step E : Draw the circle that can fit the observed radius.
A radius of 35 mm is not bad. Modify the color of the edges in red in Sketchup
So with R=35 mm, we can guess that the particle have an energy in the 600 – 800 keV range.