Les parcours dans l’air des 4 particules observables dans la chambre à brouillard sont donnés ci-dessous. Pour la correspondance {énergie cinétique-vitesse}, voir la boîte à outils relativiste. Pour la portée des rayonnements γ, voir ici.
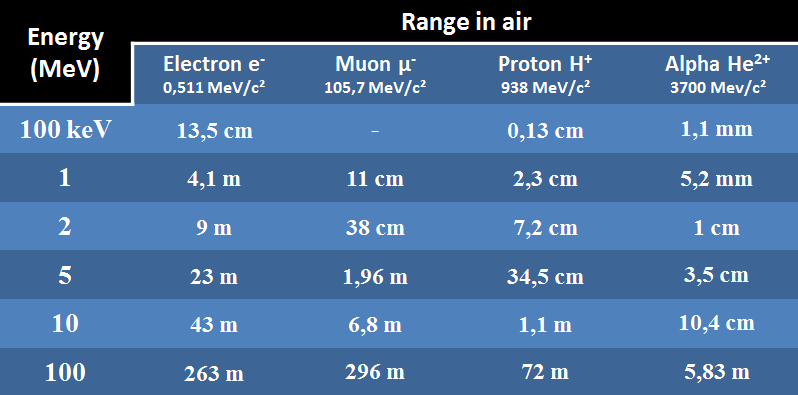
Portée des électrons, muons, protons et alpha dans l’air (d=0,00120479) simulée à partir de programmes (estar, pstar, SRIM, Casino, tables nucléaire) en fonction de leurs énergies cinétique
Les différences de parcours entre chaque particule proviennent du « dE/dx » de la particule (perte d’énergie linéique). Plus une particule perd d’énergie en traversant la matière et moins elle ira loin. Ces pertes d’énergie se traduisent par les pertes collisionnelles (ionisation des atomes), les pertes radiative (Bremsstrahlung, production de paires, interaction photoélectrique) ou nucléaire (diffusion in/élastique sur des noyaux). En fonction de la masse et de la charge de la particule, ces pertes seront plus ou moins importantes. La courbe ci-dessous illustre l’évolution de ces pertes d’énergie en fonction du type de particule traversant le volume gazeux d’un détecteur (ex ALICE ou CDF). Les pertes radiatives ou nucléaire ne sont pas prises en compte, il s’agit uniquement des pertes collisionnel de la particule avec les électrons atomique.
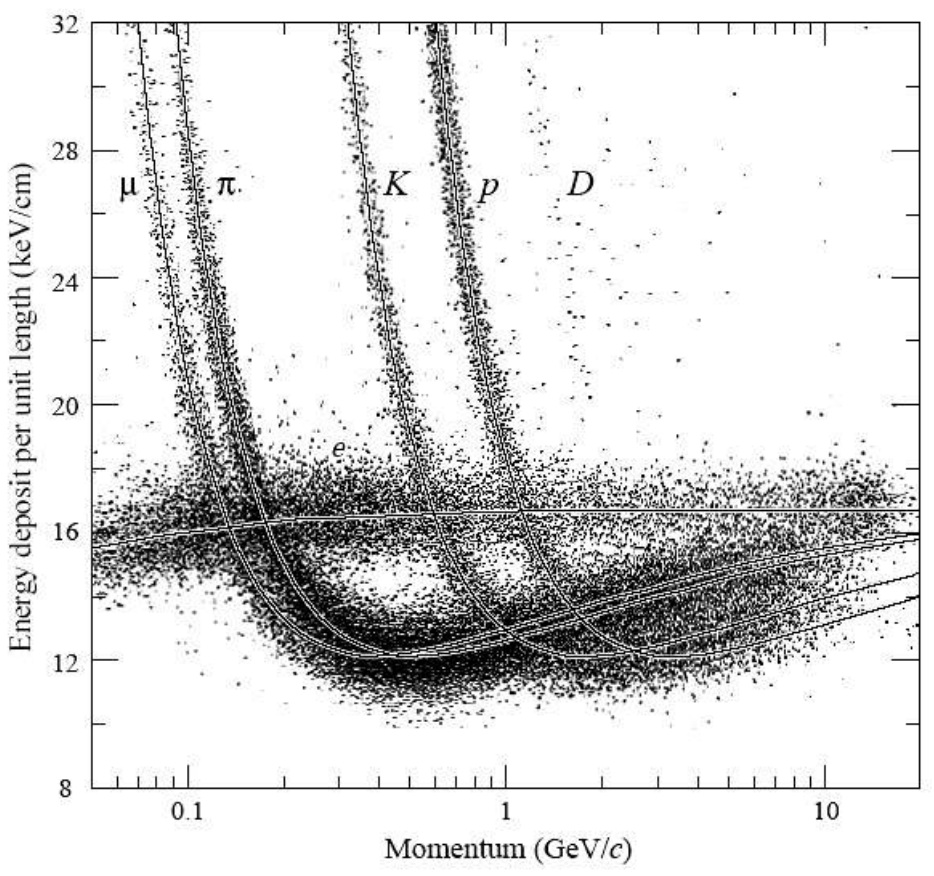
Cette courbe expérimentale montre la perte d’énergie des électrons, muons, pions, kaons, protons et deutérons dans le gaz d’un détecteur TPC (Time Projection Chamber). A momentum fixé, la perte d’énergie (keV/cm) dépend de la masse de la particule ce qui permet de les identifier. Avant le minimum d’ionisation (ici 12 keV/cm), la perte d’énergie des particules (sauf pour les électrons) est proportionnelle à 1/v²
Portées des Alpha et des Électrons :
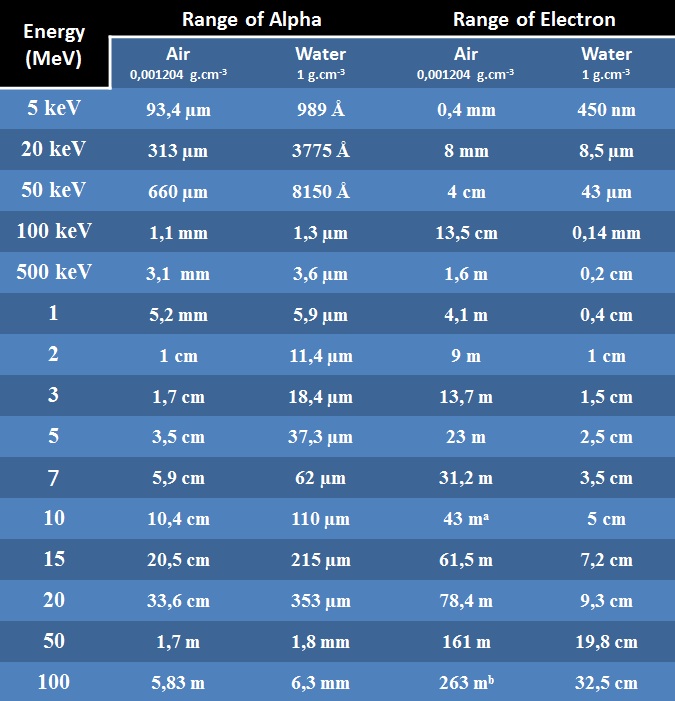
Le parcours des particules Alpha a été simulé avec SRIM. Le parcours des électrons par le programme estar. Pour les électrons, il s’agit du parcours réalisé et non la portée (cf ci dessous)
a : à partir de cette énergie, il y a environ 10 fois moins de pertes radiatives que collisionelles.
b : à partir de cette énergie, les perte radiative sont égales aux pertes collisionelles (appelé énergie « critique ») et vont rapidement dépasser ces dernières.
Un électron de 150 keV est stoppé par 52 μm de plomb. Un électron de 1 GeV, par 2,93 cm de plomb.
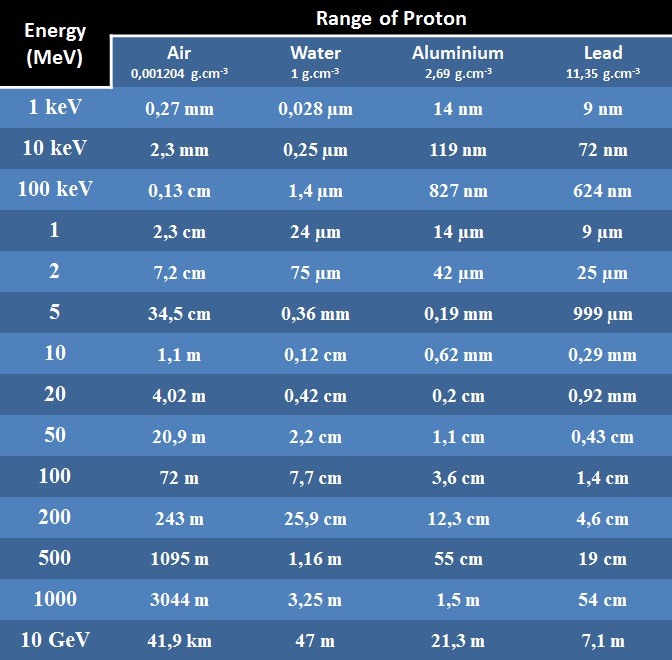
Portées des Protons :
Le parcours des protons a été simulé avec SRIM (Cliquez sur l’image)
On peut aussi calculer les portées avec le programme pstar du NIST dont un exemple de calcul est donné ici.
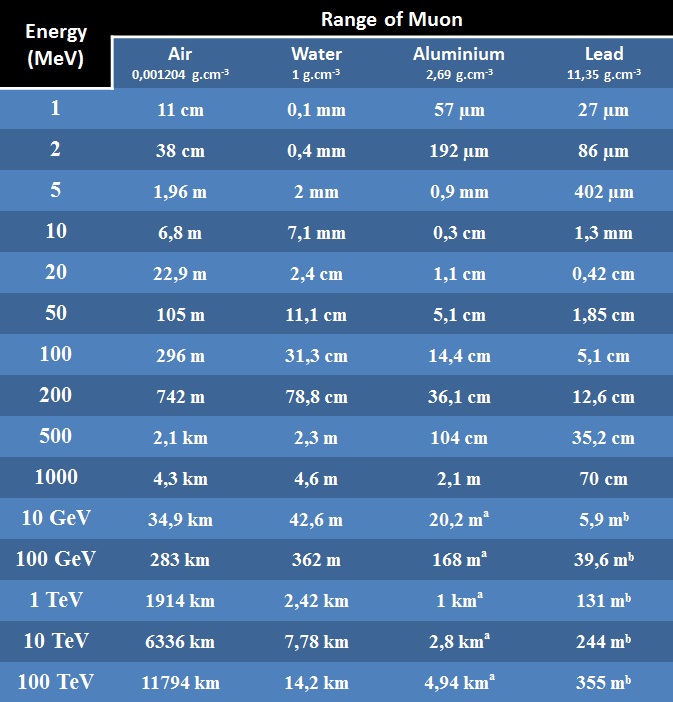
Portées des Muons :
Parcours et portée
Les parcours précédents ont été calculés à partir de la formule de Bethe, il s’agit de la longueur de matière traversé par la particule.
Une notion utile est la portée d’une particule c’est-à-dire la distance maximale « à vol d’oiseau » que peut atteindre une particule dans la matière en prenant en compte les effets de la diffusion multiple sur les noyaux ou les électrons atomiques (surtout pour les électrons).
Vue du tracé d’un électron, en blanc, se dirigeant du point A au point B.
Au début du parcours d’un électron, son énergie est élevée et les diffusions multiples se font sous de faibles angles. Vers la fin du parcours, l’énergie est plus faible et l’électron fait fréquemment des collisions inélastiques avec les électrons atomiques ou élastique avec les noyaux ce qui modifie profondément la direction de sa trajectoire qui devient erratique (cf ce chapitre).
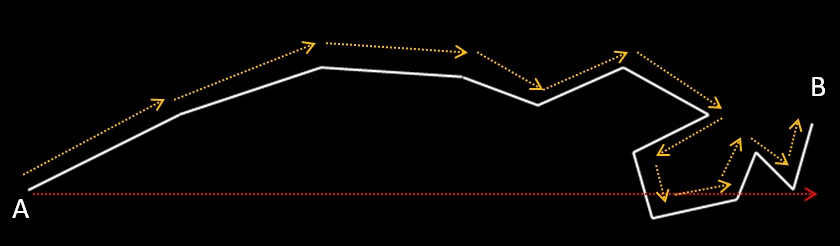
Le parcours et la portée sont deux notions différentes. La portée est la distance « à vol d’oiseau » c’est à dire la pénétration maximum de la particule dans la matière (flèche rouge). Le parcours (flèche jaune) est la distance réellement parcouru dans la matière par l’électron (le kilométrage indiqué par le compteur d’une voiture par exemple). Pour un électron, la portée est calculée avec les formules de Katz et Penfold. Le parcours (exprimé par le CSDA en g/cm²) est calculé en intégrant la formule de Bethe par rapport au pouvoir d’arrêt et à l’énergie de la particule. Il suffit de diviser la valeur de CSDA en g/cm² par la masse volumique du matériau pour obtenir le parcours en cm réalisé dans la matière par la particule. Evidemment, la portée sera toujours beaucoup plus faible que le parcours.
Pour les particules lourdes (toutes les particules sauf un électron) d’énergies pas trop faible, la distance parcouru (CSDA) est confondu avec la portée, car la masse de ces particules évite qu’elle que leurs trajectoires ne soient modifié par diffusion élastique sur les noyau : la particule « va tout droit » dans la matière.
A basse énergie, les déviations dues aux noyaux sont plus probable, la trajectoire se fait en zig zag un peu comme les électrons de basse énergie (l’image est exagéré !) et la portée devient plus faible que le parcours réel de la particule.
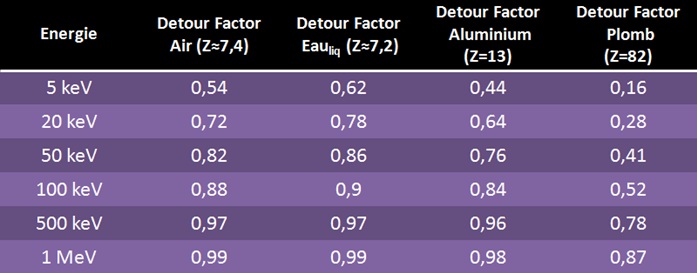
Dans les tables du NIST donnant les CSDA pour des électrons, protons ou particule alpha pour différentes énergies et matériaux, le « facteur de détour d » est défini comme le ratio entre la portée (g/cm²) et le parcours CSDA (g/cm²). La portée est calculée avec PRAL (Projected Range ALgorithm) pour les particules lourdes, à l’image des formules de Katz et Penfold pour les électrons. Quelques valeurs de facteur de détour sont données dans les tableaux ci-dessous pour des protons dans différent matériaux.
Les valeurs montrent que les protons sont plus déviés dans des matériaux à Z élevé (le Z de l’air et de l’eau à été calculé en fonction de la composition atomique du milieu). Dans l’air, les protons que l’on observe ont fréquemment des énergies supérieures à 1 MeV, leurs trajectoires seront donc droites (d=1, CSDA= portée) avec très peu de diffusions.
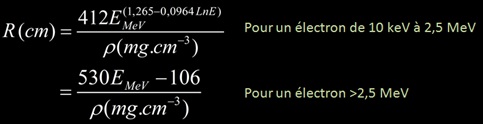
La portée des électrons peut s’estimer via les formules de Katz et Penfold.
Pour la dernière formule, on a plus simplement R(g/cm²)=0,530E-0,106. Attention cette formule n’est valable que pour des énergies maximum de 20 MeV !
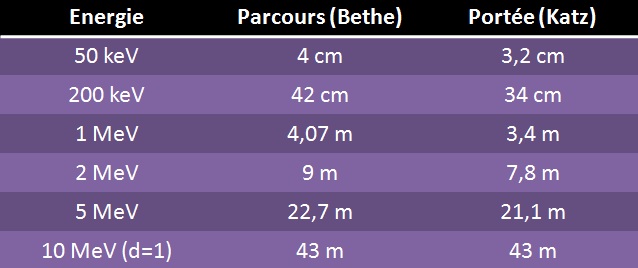
Quelques valeurs de portées pour des électrons dans l’air sont indiquées dans le tableau ci-dessous.
Le parcours (Bethe) est décliné à partir de la formule de Bethe et correspond au CSDA.
A haute énergie, un électron ne subit presque plus de diffusion multiple et les parcours et portées deviennent égales. Dans la chambre à brouillard, la majorité des électrons (du rayonnement naturel) ont des énergies inférieures au MeV. On observera donc des trajectoires erratiques du à la diffusion multiple sur les noyaux et les électrons atomiques. La diffusion multiple est proportionnelle au numéro atomique et à la densité du matériau. Plus le matériau est lourd et plus l’électron aura une petite portée et un parcours erratique à mesure que son énergie diminue.
Le programme CASINO (monte CArlo SImulation of electroN trajectory in sOlids) permet de simuler le parcours d’électrons dans différent matériau.
SRIM permet de simuler le parcours des ions chargées dans la matière.
Utilisation des tables du NIST
Quel est le parcours d’un électron de 1 MeV dans l’air ?
On se rend sur le programme estar du NIST et on choisit le matériau « air », puis on clique « submit ».
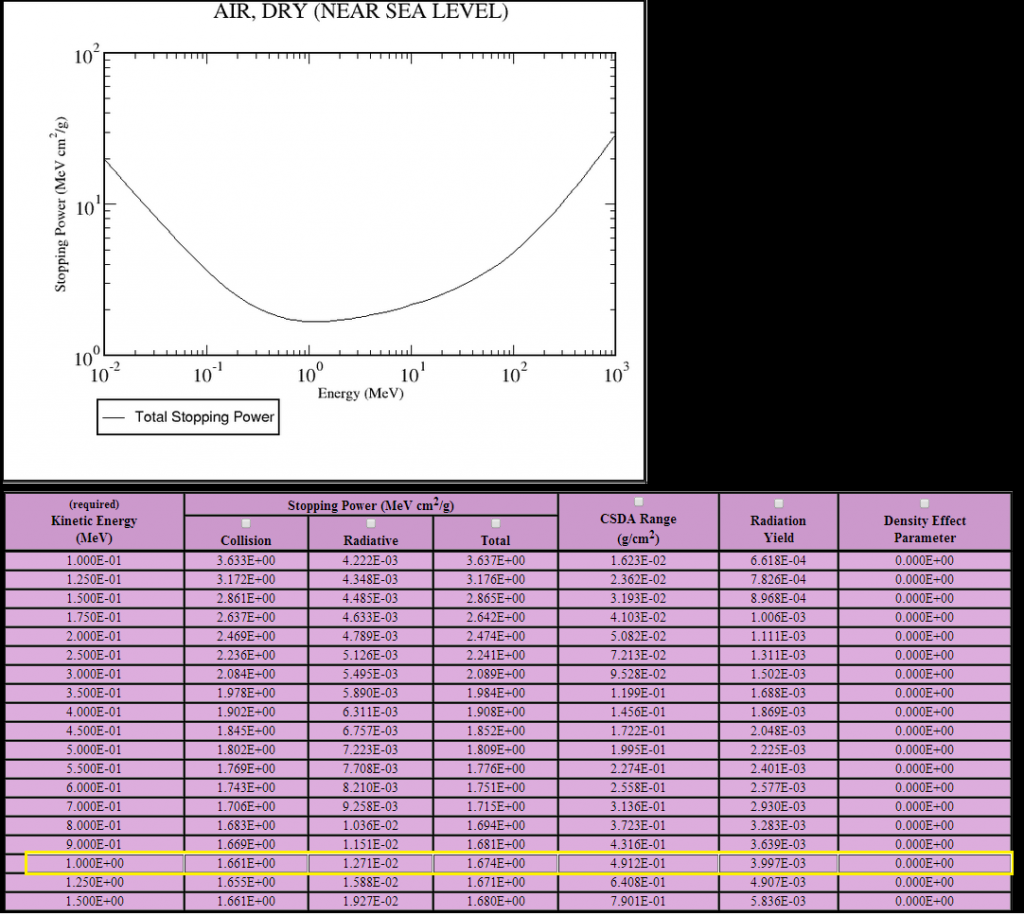
On obtient la courbe de Bethe et les valeurs de pouvoir d’arrêt et de CSDA en fonction de l’énergie :
Pour 1 MeV, le CSDA vaut 0,4912 g/cm². La masse volumique de l’air est de 0,001204 g/cm3, le parcours vaut donc 0,4912/0,001204=408 cm soit 4,08 m « avec une trajectoire en zig zag ». Pour la distance de pénétration dans la matière » à vol d’oiseau », il faut utiliser la formule de Katz : on trouve 3,4 m.
La même démarche s’applique pour calculer les parcours de protons, muons ou pions si l’on dispose des CSDA.