Les électrons représentent quasiment la totalité des traces que l’on observe dans une chambre à brouillard exposée au rayonnement naturel. Ils peuvent provenir de plusieurs sources par ordre d’importance dans une chambre à brouillard :
- par les interactions des photons dans la matière (effet photoélectrique, Compton, ou création de paires),
- par désintégration β– (création d’un électron) ou β+ (émission d’un positon, ex : 40K) d’un noyau,
- par les réarrangements nucléaire de l’atome (électrons de conversion) ou réarrangements atomique (électrons Auger),
- par la désintégration de particules comme les muons ou les kaons (cette contribution est très faible au niveau de la mer).
Les électrons et les rayonnements alpha sont les particules que l’on observe le plus souvent dans une chambre à brouillard. La vitesse des électrons est de part leur faible masse (me=mα/7240), de beaucoup supérieur à celle des particules α de même énergie. Il en résulte que le pouvoir d’ionisation des électrons est petit devant celui des rayons α ces pertes étant essentiellement proportionnel à 1/v². Une particule alpha de 1 MeV crée environ 60 000 paires d’ions par cm dans l’air alors qu’un électron n’en crée que 50 par cm d’air (à pression standard). La perte d’énergie par ionisation d’un électron est beaucoup plus faible que celui d’une particule alpha et donc à même énergie, le parcours d’un électron est bien plus grand que celui d’une particule alpha. Une particule α de 1 MeV parcourt 0,5 cm dans l’air tandis qu’un électron de même énergie à un parcours de plus de 4 m.
Autre conséquence de leur faible masse les électrons sont déviés plus facilement par les noyaux que les particules lourdes : il en résulte des pertes par Bremsstrahlung élevée ce qui à pour conséquence des trajectoires erratiques (non rectiligne) à basse énergies.
Électrons secondaires δray (delta ray)
Lorsque une particule chargée interagit dans la matière elle perd son énergie essentiellement par collisions inélastiques avec les électrons atomique du milieu. Un delta ray est un électron atomique ayant reçu suffisamment d’énergie par la particule incidente pour pouvoir s’échapper de l’attraction du noyau : c’est l’électron issu de l’ionisation de l’atome par la particule passant à proximité. Cet électron peut s’éloigner à une distance significative de la particule incidente si il dispose de suffisamment d’énergie (quelques cm, en sachant qu’un électron de 20 keV parcourt près de 1 cm dans l’air). Le delta ray perd progressivement son énergie en créant des ions au cours de sa trajectoire sur lesquels se condensent les vapeurs d’alcool matérialisant ainsi le tracé de la particule éjectée.
Nous avons vu lors de la mécanique des chocs élastiques qu’après un choc avec une particule incidente l’électron atomique initialement immobile obtient soit :
-
- 1) Vélectron = 2Vincident si melectron<<mparticule incidente (valable pour un paramètre d’impact=0). Un proton de 10 MeV peut donner au maximum 20 keV à un électron atomique ce qui représente un parcours de 8 mm dans l’air (énergie de liaison non pris en compte). Mais le nombre de delta ray avec Vélectron = 2Vincident produit par unité de longueur par le proton sera statistiquement faible comparé à la production de delta rays de faible énergie, comme décrit ici.
- 2) KEélectron=KEincident lors d’un choc frontale par une particule discernable de même masse (un positon). Cette équation reste valide si les deux particules ont la même masse (la vitesse de la particule incidente est non relativiste).
- 3) KEélectron=KEincident/2 lors d’une collision avec un électron incident non relativiste (valable pour un choc entre deux particules indiscernable de même masse avec un paramètre d’impact ≠ 0).
- 4) Un peu plus d’énergie cinétique que dans le cas 1) si l’électron incident est relativiste (melectron relativiste>m0) sans que la masse de l’électron atomique soit négligeable par rapport à celle de l’électron relativiste (cas mprojectile>mcible). Après l’interaction, on considère que la particule ayant le plus d’énergie cinétique est la particule incidente.
Un delta ray sera éjecté avec un angle compris entre 0 et 90° par rapport à la direction de la trajectoire de la particule incidente. Mesurer l’angle d’émission des delta ray permet d’identifier le sens de parcours de la particule incidente. Sur l’image du dessus le proton se dirige de gauche à droite sinon les delta ray aurait étaient émis à des angles supérieurs à 90°. On peut préciser que plus les delta rays sont proche d’un angle de 90° par rapport à la direction de la particule incidente et moins ils sont énergétiques.
Enfin concernant le rayonnement cosmique, un électron, un proton ou un muon incident n’auront pas les mêmes probabilités d’éjection de delta ray comme explicité ici. On peut retenir que pour l’éjection d’un delta ray d’énergie donnée un muon à plus de chance de créer ce delta ray qu’un proton, et un électron plus de chance qu’un muon.
.
Electrons in expansion cloud chambers
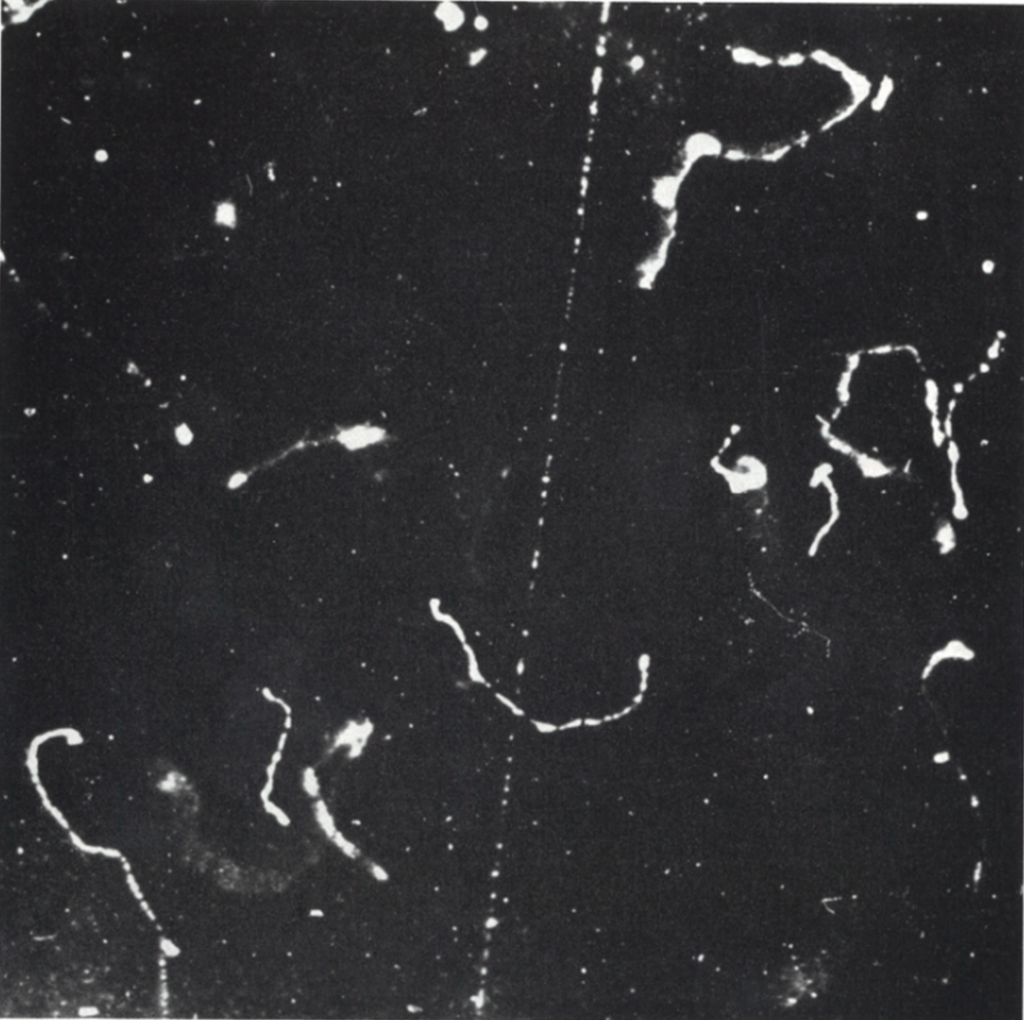
Les images ci dessous sont tirés du livre remarquable de Bothe, Gentner et Maier-Leibniz, publié en 1940 : the Atlas of Typical Cloud Chamber Images. Elles sont toutes prises dans une chambre à expansion de Wilson.
Les électrons de faibles énergies décrivent des trajectoires irrégulièrement courbées par suite de la diffusion multiple sur les noyaux ou les électrons atomiques (les angles de diffusion sont inversement proportionnel à la vitesse de la particule). Les électrons rapides (>200 keV) décriront des trajectoires rectilignes dans l’air. La photo montre des électrons lents libérés dans le gaz par des rayons X (effet photoélectrique) et d’autre part un électron rapide (le tracé droit vertical). L’ionisation produite est plus forte le long des trajectoires courtes et courbées que le long de la longue trajectoire rectiligne car les pertes d’énergie par ionisation (dE/dx) sont inversement proportionnel au carré de la vitesse de la particule.

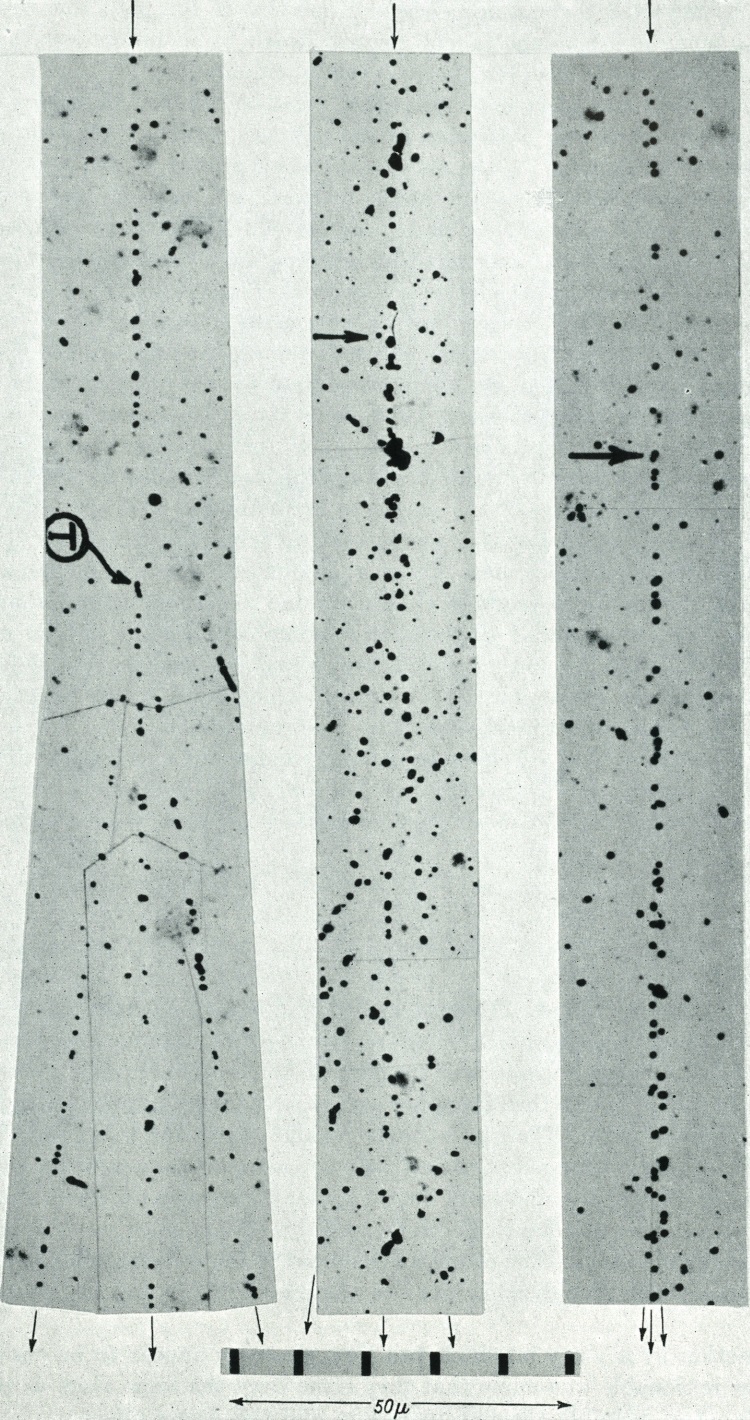
Photo du dessus : Vue rapprochée de la trajectoire d’un rayon beta sous 400 mm Hg. Une accumulation d’ions au milieu de la trajectoire est visible (1932). Photo du dessous : Agrandissement 3x de la trajectoire d’un électron sous 200 mm Hg. Les paires d’ions sont visibles (1923).
Lorsqu’une particule chargée traverse la matière elle perd de l’énergie en ionisant un atome. L’électron libéré se fixe très rapidement sur une molécule neutre formant un ion moléculaire négatif qui avec l’ion positif restant constitue une paire d’ions. Dans le cas des chambres à expansion si l’on laisse le temps de diffuser aux ions formés par le passage d’un rayon béta, c’est-à-dire de se séparer les uns des autres en l’absence de champ électrique avant que n’ait lieu la détente, chaque ion apparaîtra comme une gouttelette séparée. On distingue sur la photographie inférieure les paires d’ions créée apparaissant sous la forme de deux gouttelettes distincte.
La photographie supérieure montre un phénomène que l’on voit souvent dans les chambres à brouillard et qui apparaît le plus souvent sur les trajectoires des particules : des agrégats de gouttelettes provenant d’une accumulation locale d’ions. Les électrons libérés des atomes par le passage d’une particule chargée ont des vitesses différentes et une partie d’entre eux sont capable d’ioniser à leur tour. Les accumulations d’ions proviennent d’un électron secondaire qui à été capable de créer un assez grand nombre de paires d’ions. Lorsque l’énergie des électrons secondaires est encore plus élevée ils sont capable de s’éloigner de la trajectoire de la particule incidente en formant leur propre trace. On dénomme ces électrons secondaires de « grandes » énergies des delta ray.
Diffusion des électrons par des électrons atomiques
Choc d’un électron sur un électron atomique. L’électron éjecté devient un « delta ray ». Pas de champ magnétique (1935).
La photo montre le choc d’un électron de 56 keV sans champ magnétique sur un électron atomique. Cette fois ci l’énergie cinétique cédé à l’électron est suffisante pour que ce dernier fasse sa propre trace en ionisant d’autre atome : c’est un delta ray. Après le choc, l’électron incident et le delta ray ont sensiblement la même énergie. Au cours d’un choc électron-électronatomique et lorsque la vitesse de l’électron incident n’est pas trop grande de manière à ce que sa masse soit proche de celle au repos, l’énergie cinétique maximum transférable est égale à Eincident/2 ce qui est le cas sur cette photo. Un delta ray peut au maximum avoir une vitesse égale à 2 fois celle de la particule incidente si celle-ci est une particule massive.
A gauche : rayon delta de 40 keV libéré par un électron de 300 keV, venant d’en bas, avec un champ magnétique de 300 Gauss. A droite : choc d’un électron de 1,6 MeV (1935).
Les rayons bêta ayant la même masse que les électrons atomique les angles de diffusion après le choc seront de 90° comme on peut le voir sur les photos (sur la photo de gauche, on observe un rayon delta de faible énergie). Lorsqu’un électron est relativiste c’est-à-dire proche de la vitesse lumière, sa masse vaut m=γm0 avec γ le facteur de Lorentz (pour v=0.14c, soit Ec=5,1 keV, γ=1.01 ; γ=1.5 pour Ec=255 keV). La masse des deux particules qui collisionnent ne sont plus les même (melectron relativiste>melectron atomique) et l’angle après le choc est inférieur à 90°. La photo de droite montre la création d’un δray d’énergie importante à partir d’un rayon bêta incident de 1.6 MeV. L’angle est ici de 60°.
Diffusion des électrons par des noyaux

Diffusion d’un rayon béta de 0.25 MeV dans le méthane sous 1.5 atm, avec un champ magnétique de 300 gauss. Au centre de l’image, le parcours d’un électron est brusquement dévié par un noyau
Lorsque un électron collisionne avec un électron atomique l’électron incident est dévié de sa trajectoire ce qui se traduit par un transfert d’énergie à l’électron atomique qui devient un delta ray. L’angle maximum entre les particules diffusées est alors de 90°. Cependant il arrive parfois que les électrons subissent des changements de direction brusques et notable (des angles de déviation supérieur à 90° sont possibles) sans donner naissance à un électron secondaire. On attribue ce phénomène à une diffusion par un noyau atomique. Le noyau ayant une masse 1836A fois plus grande que l’électron, ce dernier ne cède que très peu d’énergie au noyau. On qualifie donc la collision d’élastique. On peut observer ce phénomène dans la photo ci dessus et dessous.
Comme vue dans les paragraphes théoriques, la diffusion par les noyaux est beaucoup plus fréquente dans les éléments lourd que léger et lorsque la vitesse de la particule est faible. A grande énergie, les électrons déviés par les noyaux font des collisions inélastiques c’est-à-dire qu’une partie de l’énergie est perdu sous forme de rayonnement de freinage ou « Bremsstrahlung ». Ces pertes sont proportionnel à la vitesse et au numéro atomique du noyau heurté.
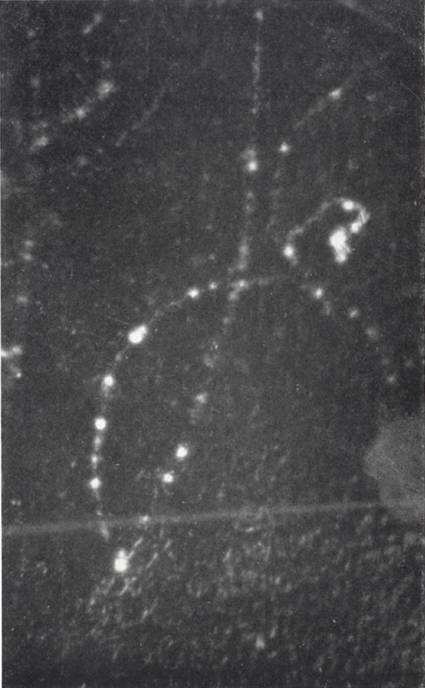
Diffusion inélastique d’un électron de 2.5 MeV venant par le haut sur un noyau dans le Xénon sous un champ magnétique de 1300 gauss. L’angle de diffusion est très important : les pertes par Bremsstrahlung sont élevées. (1936)
La photographie ci dessus montre un tel exemple de collision inélastique. L’électron incident vient du haut et dispose de 2.5 MeV d’énergie cinétique. Le rayon de courbure est grand (la trajectoire se rapproche d’une ligne droite) car la vitesse de la particule est élevée et n’est donc peu soumise à l’influence du champ magnétique. Après le choc avec un noyau, l’électron est quasiment rétrodiffusé et décrit un rayon de courbure beaucoup plus faible que précédemment. Son énergie à donc diminuée drastiquement, or nous avons vu que les transferts d’énergie au noyau lors de collision avec des électrons était quasiment nulle : la diffusion à fait perdre près de 2.2 MeV d’énergie cinétique qui a été convertie en rayonnement X de freinage.

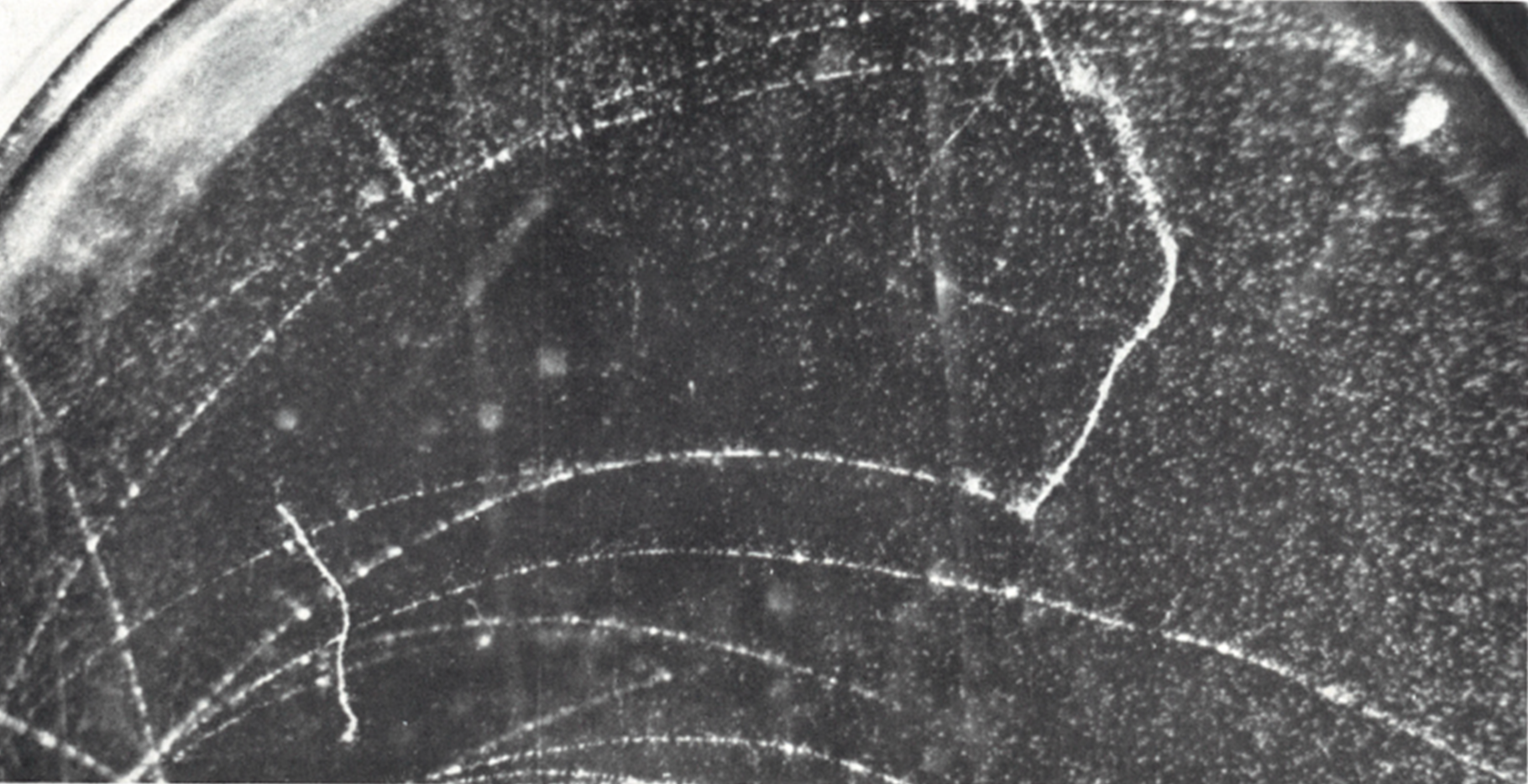
Electron rapide perdant son énergie par ionisation et radiation (Bremssthralung). Champ magnétique 1T, Argon 50%, Helium 50%. Les lignes parallèle sont les fils pour le champ électrique. La chambre mesure 41 cm de diamètre pour une profondeur de 15 cm. La taille de la plus grande spire mesure environ 12 cm de diamètre. Radiation Laboratory, Berkeley
La photographie ci dessus montre un électron dont l’énergie initiale est de 16.9 MeV. Il prend naissance dans la création d’une paire dans le gaz au point marqué par la flèche ; sa trajectoire décrit 36 spires dans le champ magnétique. Au point où la trajectoire cesse d’être visible l’énergie de l’électron est tombé à 12.4 MeV. Le chemin parcouru est alors de 1030 cm ce qui correspondrait à une perte d’énergie par ionisation de seulement 2.8 MeV. La perte d’énergie réelle, qui s’élève à 4.5 MeV à eu lieu par rayonnement de freinage. Le rayon de courbure subit des variations brusques comme on peut le voir à partir de la 5 éme et 15 éme spire, due à une émission de rayonnement de freinage importante.

Ecran de plomb de 0.5 mm (au milieu de la photo), électrons (venant du haut, en bas) de 2-4 MeV avec un champ magnétique.
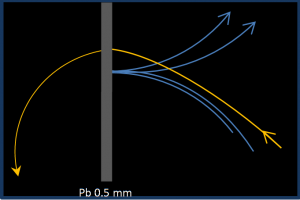 Les photographies suivante montrent les phénomènes qui apparaissent lors du passage des rayons béta à travers des écrans. Dans la photo ci dessus deux rayons (en bleu) situés très près l’un de l’autre subissent à l’intérieur de l’écran des diffusions telles qu’ils ressortent vers l’arrière (rétrodiffusion) avec une énergie moindre. Deux autres électrons traversent l’écran ; le premier (en jaune) perd une grande partie de son énergie par rayonnement de freinage comme le montre la courbure magnétique de sa trajectoire après avoir traversé l’écran. Le second électron (toujours venant du haut) ne subit qu’une légère déviation (la matière ayant une structure lacunaire, un électron qui passe très près d’un noyau en subissant une grande déviation reste moins probable que de petites déviations).
Les photographies suivante montrent les phénomènes qui apparaissent lors du passage des rayons béta à travers des écrans. Dans la photo ci dessus deux rayons (en bleu) situés très près l’un de l’autre subissent à l’intérieur de l’écran des diffusions telles qu’ils ressortent vers l’arrière (rétrodiffusion) avec une énergie moindre. Deux autres électrons traversent l’écran ; le premier (en jaune) perd une grande partie de son énergie par rayonnement de freinage comme le montre la courbure magnétique de sa trajectoire après avoir traversé l’écran. Le second électron (toujours venant du haut) ne subit qu’une légère déviation (la matière ayant une structure lacunaire, un électron qui passe très près d’un noyau en subissant une grande déviation reste moins probable que de petites déviations).

Rétrodiffusion répétée d’un électron par un écran de plomb de 0.2 mm. L’énergie initiale de l’électron est de 0.35 MeV, le champ magnétique est de 1400 gauss, le diamètre de la chambre 11 cm (Leprince-Ringuet, 1936).
La photographie ci dessus montre un électron (venant par le bas) dont la trajectoire courbé provient de l’effet du champ magnétique. L’électron rencontre une première fois un écran de plomb, est rétrodiffusé, est à nouveau courbé par le champ puis rencontre une nouvelle fois l’écran de plomb faisant une deuxième rétrodiffusion. Le processus se répète une dernière fois.
Les positons

Découverte du positon. Champ magnétique de 1,5T, diamètre de la chambre 15 cm. Un positon de 63 MeV traverse un écran de plomb de 6 mm dont il sort avec une énergie de 23 MeV.

Carl Anderson travaillant sur l’électroaimant de sa chambre à brouillard (au milieu des deux bobinage, en blanc) à Caltech. Un générateur provisionnait 600 kW de puissance électrique pour alimenter l’aimant. Les bobines étaient refroidis avec de l’eau.
Anderson prit cette photo en 1933 à Caltech en étudiant le rayonnement cosmique dans un champ magnétique très intense (15.000 gauss). Sur la photo, il résulte de la courbure de la trajectoire que la particule à au dessus de l’écran une énergie plus faible qu’en dessous (plus une particule est lente et plus elle subit l’influence du champ magnétique et plus sa trajectoire se rapproche d’un cercle). La particule doit donc être venu d’en bas, en traversant la chambre de bas en haut, et le sens de la courbure indique qu’elle porte une charge positive. Par sa densité d’ionisation et son comportement au passage de l’écran, elle ne se distingue pas d’un électron. Anderson conclut d’après cette photographie à l’existence d’un électron « positif » ou « positon ». Dans le rayonnement cosmique les positrons proviennent de la matérialisation des rayonnements γ (création de pair), de la désintégration des kaons, des pions et des muons. Certain noyaux radioactifs (ex Na22) se désintègre par émission de positron (β+).
.
.
Diffusion des positons par des électrons atomiques

Choc d’un positon de 250 keV (venant du bas) avec un électron. Chambre remplie de méthane sous 1.5 atm avec un champ magnétique de 300 gauss.
En ce qui concerne l’ionisation les positons se comportent exactement comme les électrons. Une différence se manifeste cependant dans le choc des positons avec des électrons : alors que dans un choc électron-électron les partenaires sont indiscernable, dans un choc positon-électron le positon conserve sa personnalité du fait de sa charge. Les photos ci dessus et en bas à gauche montrent des exemples de tels chocs. Sur la première, le positon (venant d’en bas et courbant vers la droite) conserve après le choc avec un électron atomique un peu plus de la moitié de son énergie initiale. Le delta ray est dévié vers la gauche par le champ magnétique.

A gauche : choc d’un position de 80 keV avec un électron avec transfert de la quasi totalité de la quantité de mouvement.
A droite : Un positon de 210 keV heurte simultanément 2 électrons. La chambre est remplie de méthane sous 1.5 atm avec un champ magnétique de 300 gauss (1951).
La photo de gauche montre un exemple assez rare : un choc quasiment frontale avec un paramètre d’impact presque égale à 0 entre un positon (venant du bas, dévié vers la droite) et un électron atomique. Après le choc, le positon lui reste environ 5 keV d’énergie, ce qui forme l’accumulation d’ions au point d’impact. L’électron percuté repart avec quasiment la totalité de l’énergie cinétique du positon, en étant dévié vers la gauche du fait de sa charge. La trajectoire résultante décrit un « S ». Si le choc aurait été parfaitement frontale (b=0) le transfert d’énergie cinétique aurait été total.
La photo de droite montre un exemple encore plus rare : un positon (dévié vers la droite) heurte simultanément deux électrons. Les deux delta rays déviés vers la gauche emporte chacun une grande quantité d’énergie.
Diffusion des positons par des noyaux
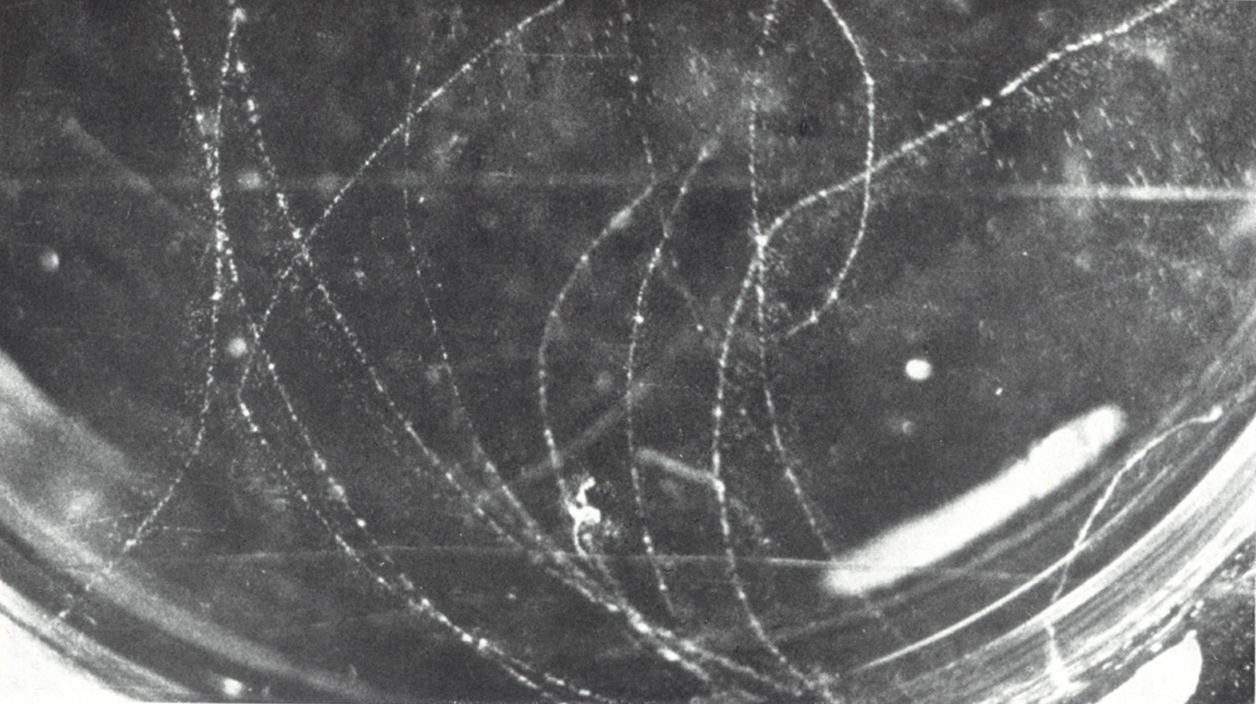
Diffusion d’un positon de 0.2 MeV sous un angle de 60° (mêmes conditions expérimentale que précédemment).
Les positons peuvent, comme les électrons, être diffusé par de grand angle si ils se rapprochent trop des noyaux. Sur les photos, les positons viennent du bas et sont dévié vers la droite. Au choc, on observe pas de delta ray, il s’agit bien d’une diffusion par un noyau, avec perte d’énergie par rayonnement de freinage. Sur les deux photos ci dessous, ces pertes sont élevés comme on peut le voir après le choc avec la diffusion multiple prononcée vers la fin des trajectoires. Il convient de préciser que la théorie de Dirac introduit des différences entre électrons et positons en ce qui concernent leur diffusion sur des noyaux lourd, sous de grand angle : les positons sont moins fortement diffusés que les électrons.
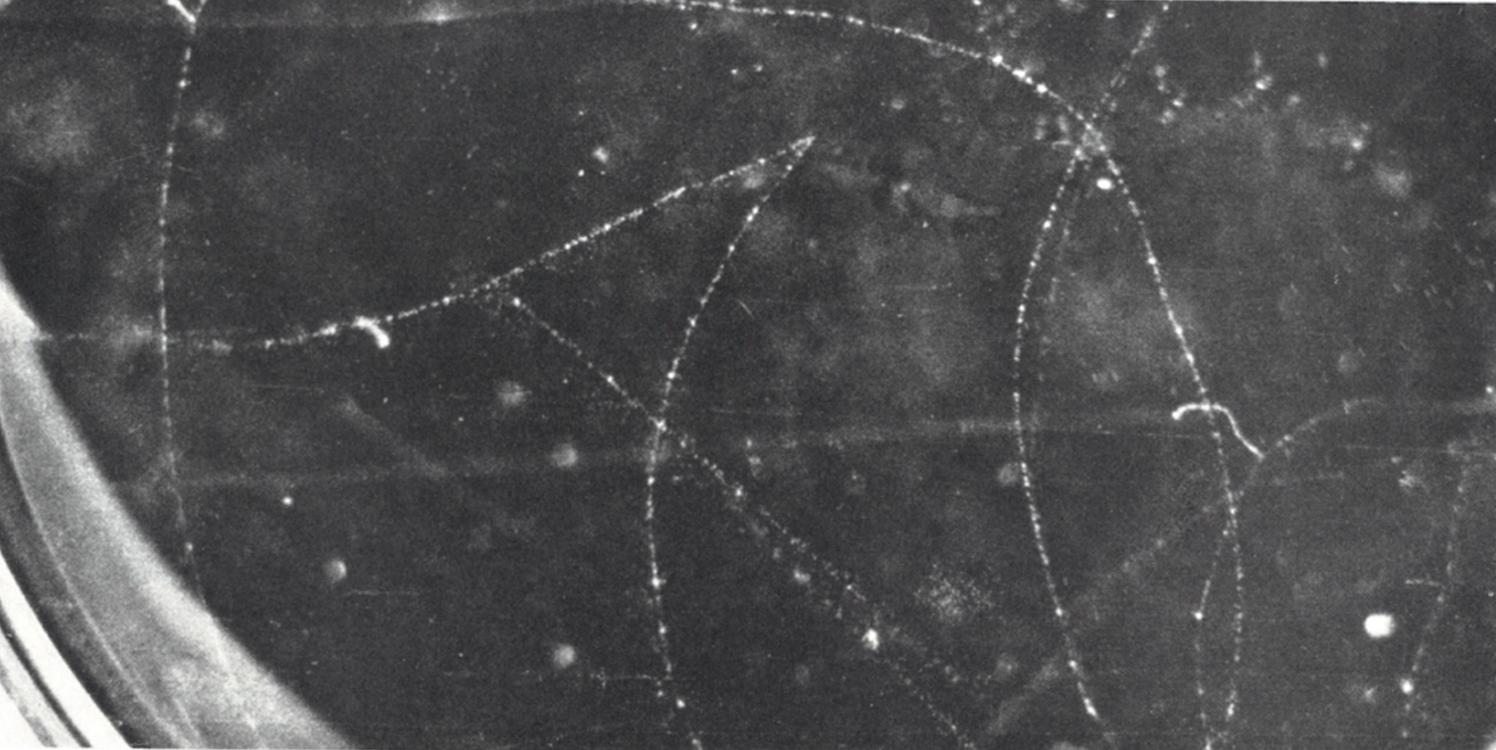
Diffusion inélastique d’un positon de 90 keV sous un angle de 145°(mêmes conditions expérimentale que précédemment).
Diffusion inélastique d’un positon de 200 keV. Après le choc, l’énergie du positon est d’environ 40 keV.
.
Electrons de conversion et Auger
Electron de conversion interne des rayons γ issu du radon 219 gazeux. Les électrons Auger sont aussi visible. Champ magnétique 380 gauss (1938).
Lors de la désintégration α du Radon 219 en Polonium 215 il se forme aussi des noyaux de 215Po excités. Le noyau peut se désexciter en émettant un rayonnement gamma (γ) ou transférer cette énergie de désexcitation à un électron du cortège électronique. Celui ci quitte l’atome avec une énergie égale à la différence entre l’énergie d’excitation du noyau et l’énergie de liaison de l’électron à sa couche : c’est le phénomène de conversion interne des rayons γ. L’émission d’électron de conversion est un processus en compétition avec la désexcitation par émission de rayonnement gamma.
C’est ce que l’on observe sur l’image ci dessus avec la désintégration du Radon 219 en Polonium 215 et du Polonium 215 en Plomb 211. Ces désintégrations se font par émission alpha. Etant donné la courte demi-vie du Polonium 215 (1,78 μs) les rayons α du Radon et du Polonium semblent issus du même point (le phénomène est identique avec le Radon 220 (thoron) se désintégrant en Polonium 216 puis en Plomb 212 décrit dans les expériences).
Sur les photographies on voit sortir du même point des électrons ayant des énergies de plusieurs centaines de keV (un électron de 20 keV parcours 1 cm dans l’air et dans le cas de la désintégration du 219 Rn, celui ci émet à 80% un alpha de 6,81 MeV qui à un parcours maximum dans l’air de 5,6 cm, ce qui donne l’échelle). Ces électrons proviennent de conversions internes.
On voit apparaître en outre de très courtes trajectoires à l’origine du point d’émission : ce sont des électrons Auger. Après l’émission de l’électron de conversion il manque un électron au cortège électronique. Cette lacune va être comblée par un électron des couches supérieures qui va se désexciter vers le niveau de la lacune afin de la combler. L’énergie de désexcitation de l’électron va servir à éjecter un autre électron des couches supérieures à la lacune, plutôt qu’émettre un rayon X. L’émission d’électron Auger est un processus de désexcitation de l’atome en compétition avec la désexcitation par émission de rayon X. L’énergie d’un électron Auger sera toujours très inférieure à celle d’un électron de conversion car les réarrangements nucléaire se font avec des transitions bien plus énergétique que dans les réorganisations du cortège électronique.
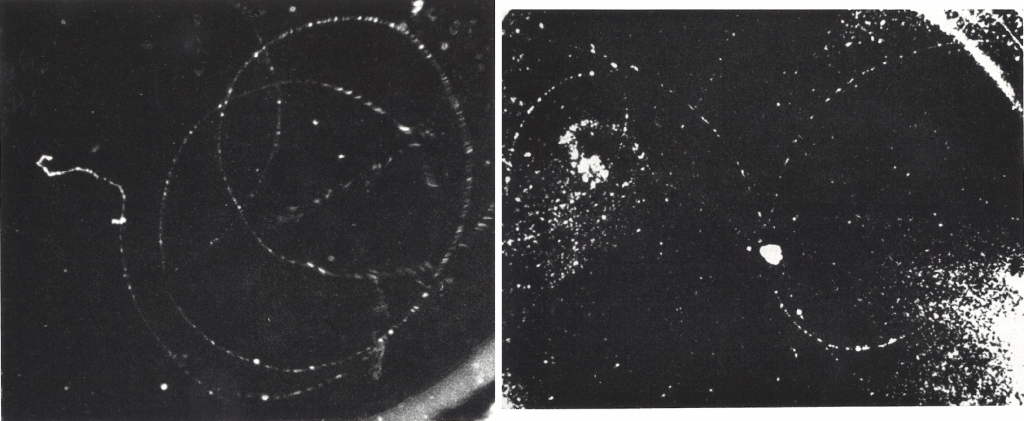
A gauche : Conversion interne au cours de la désintégration béta du Xenon 135 ou 133, avec émission d’électron Auger, champ magnétique 530 gauss. A droite : Paire d’électron-positon provenant de la désexcitation d’un noyau d’Arsenic par émission gamma (2,2 MeV). Champ magnétique 714 gauss, diamètre de la chambre 18 cm
Le phénomène de conversion interne se présente chez les émetteurs β aussi bien que chez les émetteurs α. La probabilité de conversion interne diminue en général quant le numéro atomique devient plus faible. Dans la chambre de gauche celle ci contenait des traces de Xénon radioactif. On voit trois particules issues du même point : on peut les identifier l’une comme une particule β (électron de désintégration), la deuxième comme un électron de conversion et la dernière, toute petite, comme un électron Auger.
Si l’énergie de désexcitation du noyau est plus grande que 1,02 MeV il peut y avoir formation d’une paire électron-positon par l’intermédiaire d’un rayonnement gamma au lieu de l’émission d’un électron de conversion. Cet effet est très faible dans les corps naturels radioactifs vis à vis de l’émission d’électron de conversion. Cependant l’effet de formation de paire ne dépend pratiquement pas du numéro atomique alors que l’effet photoélectrique interne (émission d’électron de conversion) croît avec ce numéro. La formation de paire se trouve donc favorisée dans les éléments radioactifs artificiel léger. Dans la chambre de droite il y avait une feuille roulée trés mince, d’Arsenic radioactif. En même temps qu’un électron de désintégration β (dirigé vers le bas) apparaît, une paire e–-e+ est formée, provenant de l’énergie de désexcitation du noyau portée par un rayonnement gamma.
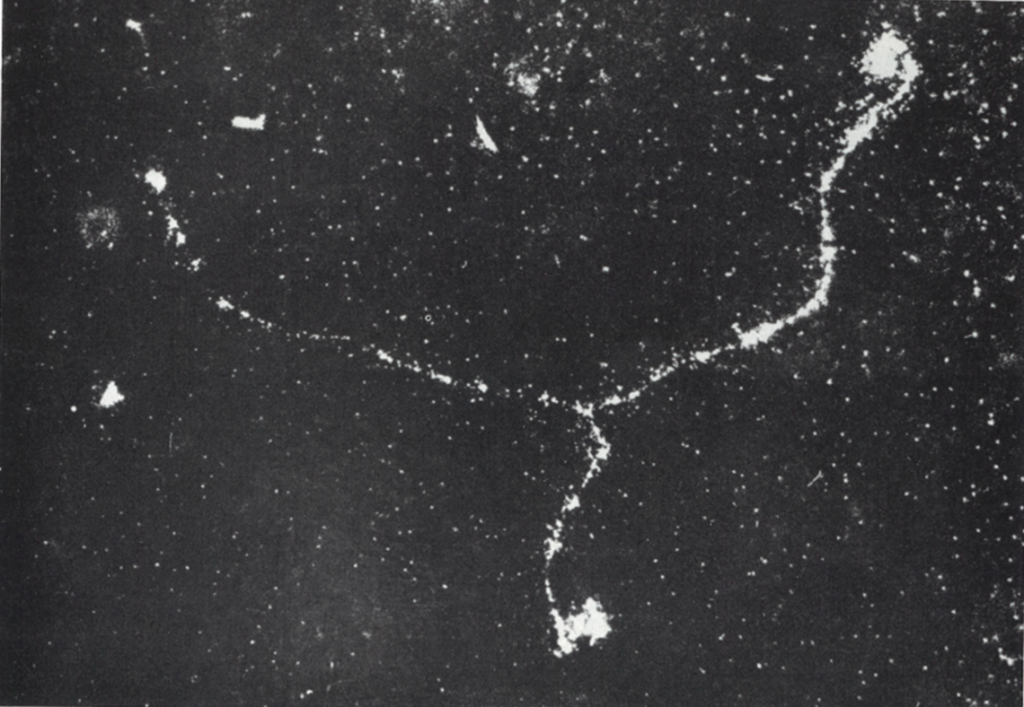
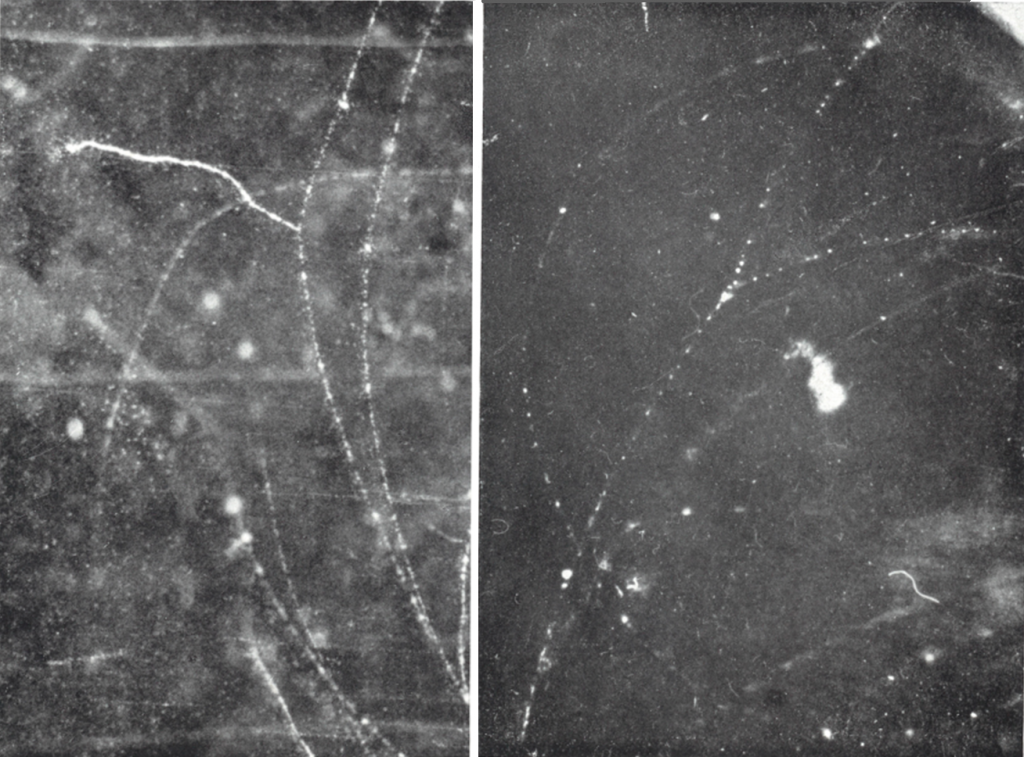
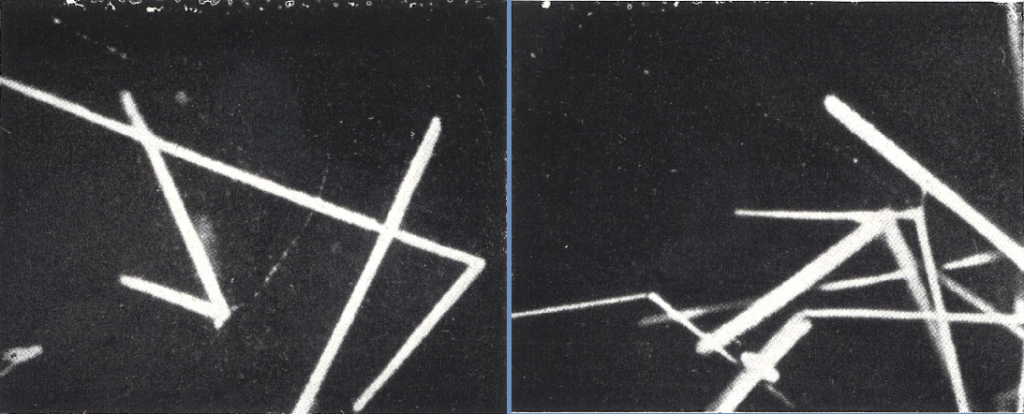
Trident production
In addition to losing energy by bremsstrahlung, fast electron can also produce pairs of electrons by interaction with the electro-magnetic field of a nucleus, so that a single fast electron approaches a nucleus and three emerge (see picture below). This event was first observed in photographic emulsions in 1949.
Left : The tracks of the incoming electrons and the point of origin of the pairs are indicated by arrows. The events are of relatively low energy so that there is a wide angular difference of the tracks. In theses circumstances, it is improbable that a pair produced by bremsstrahlung of the incoming electron will originate precisely on the line of motion of the parent electron.
Trident production must be distinguished from other processes which can sometimes give apparently similar effects. When an electron of great energy produce a photon by bremsstrahlung, the angular divergence in the direction of motion of the two products may be very small. If by chance, the photon materializes after traversing only a short path in the emulsion (in air the distance would be 2000x longer), the pair may originate at a point which is apparently coincident with the track of the primary electron. So at very high energy, it is to be expected that an appreciable proportion of the pairs due to bremsstrahlung will originate at points separated from the parent electron track by distances less than can be resolved under the microscope, and will thus give rise to ‘pseudo tridents’.
When the energy of the primary electron is low, the cross-section for the production of tridents is low, about 1% of that for bremsstrahlung but this value is considerably higher at high energy (approx. 6% between 1 and 10 GeV, 70% at 100 GeV).
.